On Robust Control of Adaptive Algorithms for Acoustic Echo Cancellers

The main purpose of the paper was to investigate robust adaptive echo cancellation algorithms in hands-free scenarios to achieve an understanding of its performance and also its effects on Double-talk (DT).

1. Introduction

DT is a major issue present in acoustic echo cancellation (AEC). It occurs when both the far-end and the near-end speakers speak simultaneously. Many attempts have been made to alleviate the isruptive effects of DT; these include the use of DT detection schemes, robust daptive AEC, step-size control, state-space representation ([1], [2]). The scheme f extending robust algorithms to an acoustic hands-free environment as proposed in [3] became the motivation for this paper. Robust adaptive echo cancellation in particular, is an interesting approach because if appropriately combined with a good double-talk detector (DTD) it could offer a noteworthy solution in overcoming the problems of DT [2]. This approach was used for line echo cancellers (LEC) [3]. Thus, by extending the method to acoustic hands-free scenarios, it may prove very valuable in the long term goal of eliminating the problems caused by DT.
As shown in ([4], [5]), faster convergence can be achieved by using algorithms like Proportional Normalized Least Mean Squares (PNLMS) and PNLMS++. For LEC, it is reasonable to assume that the echo path is sparse (i.e. many coefficients are zero), and try to identify only the non-zero active coefficients. This is the idea behind the PNLMS algorithm which is a modification of the NLMS. Thus, higher convergence rate is achieved by using the fact that the active part of network echo path is usually much smaller (4-8 ms) compared to 64-128 ms of the whole echo path that has to be covered. In PNLMS, an adaptive individual step-size is assigned to each filter coefficient.
However, this algorithm does not utilize the fact that the speech signal is a correlated signal. If this is taken into account, further increase in convergence rate can be achieved; this thought leads to the Affine Projection Algorithm (APA) ([6], [7]).
Besides the convergence rate, an important aspect of an echo canceller (EC) is its performance during DT. To inhibit the divergence of the EC the standard procedure is to use a level based DTD [8]. Whenever DT is detected the step-size of the adaptive filtering algorithm is set to zero thus inhibiting the adaptation. Unfortunately, during the time required by the DTD to detect DT, the EC often diverges. This is because even a few undetected amplitude samples perturb the echo path estimate considerably [3]. Once this happens, the coefficients are frozen in a poor state for at least the hangover time before adaptation can be resumed.
The key to the solution is a combination of a DTD with robust statistics. Such approach is based on introducing a scaled nonlinearity into the adaptive algorithm. The nonlinearity limits the impact of large disturbances on the coefficient setting, but also reduces the convergence rate. The idea was developed for a subband echo canceller in [9].
The main objective of this work investigates the type of parameters that can be used in robust algorithms to offer robust performance and their effect on DT. As the performance of the robust Proportionate Affine Projection Algorithm (PAPA) is shown to be better than other algorithms in network echo cancellation ([3], [10], [11]), investigation is performed on the parameters of the robust PAPA algorithm.
 

2. Adaptive Algorithms and Notations

In derivations and descriptions the following notations are used (see also Fig. 1).  

Fig. 1 Block diagram of the echo canceller and DTD [3].

The excitation vector is denoted x_n=[x_n,...,x_n-L+1]^T, where x_n is the far-end speech signal. v_n+ w_n is the background noise mixed with the near-end speech. The microphone signal is denoted y_n. The residual echo is e_n=y_n-h_n^Tx_n, where h_n=[h_0,n,...,h_L-1,n]^T is the estimated echo path. Here L is the length of the adaptive filter. 

 2.1 The Proportionate Algorithms

The step-sizes in the PNLMS algorithm are calculated from the last estimate of the filter coefficients so that a larger coefficient receives a larger weight, thus increasing the convergence rate of that coefficient. This has the effect that active coefficients are adjusted faster than non active coefficients (i.e. small or zero coefficients). This algorithm is described by the following equations: 

(1)

(2)

 G_n is a diagonal matrix which adjusts the step-sizes, μ is the overall step-size parameter, and δ is a regularization parameter which prevents division by zero and stabilizes the solution when speech is used as input signal. The diagonal elements of G_n+1 are calculated as follows, [4],

(3)

(4)

 Parameters δ_p and ρ are positive numbers with typical values δ_p = 0.01, ρ= 5/L.

A variant of this algorithm is called the PNLMS++ [5]. There, for odd-numbered time steps the matrix G_n is derived as above, while for even-numbered steps it is chosen to be the identity matrix ( G_n = I), which results in the NLMS algorithm. The alternation between NLMS and PNLMS iterations has several advantages compared to using just the PNLMS technique (in the case of pure PNLMS, as the large weights adapt, the remaining small coefficients adapt at a rate slower than NLMS), e.g., the PNLMS++ algorithm is much less sensitive to the assumption of a sparse impulse response.

 2.2 The Robust NLMS and PNLMS++ Algorithms

The NLMS and PNLMS++ algorithm can both be made robust to large disturbances by modification of the criteria on which they are based [3]. The robust NLMS algorithm is given by,

(5)

 where Ψ(^.) is a limiter function,

(6)

 and the adaptive scale factor, s_n, is defined as,

(7)

 where λ controls the scale factor. β is a normalization constant, it dependents on k₀,

(8)

 where erfc(^.) is a complementary error function defined as,

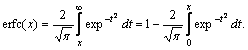(9)

 As with the Geigel DTD (which is an essential component in the robust algorithms) [8], it is useful to introduce a hangover time to control scale updating. When the DTD detects DT, adaptation of s_n should be inhibited for a specific time, preferably al long as the DTD hangover time, Thold, [10]:

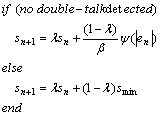(10)

The PNLMS algorithm can be made robust in an exactly analogous manner, yielding the equation

(11)

Alternating the iterations with G_n as given in (3) and the identity matrix then yields the robust PNLMS++ algorithm.

 2.3 The Robust  Proportionate APA (PAPA)

Let y_n=[y_n,...,y_n-p+1]^T, be a vector of samples y_n and X_n=[x_n,...,x_n-L+1]^T the excitation matrix, where p is the projection order. A residual echo vector e_n=y_n-X_n^Th_n, and PAPA is then given by,

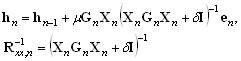(12)

where G_n is as defined in equation (2) and R is a weighted estimate of the inverse correlation matrix of the input signal. This matrix “whitens” the input data, X_n, and thus the convergence rate of the adaptive filter is increased. With G_n = I and δ=0, the equation (14) reduces to the standard APA [6].
A robust version of PAPA (and hence of APA) is obtained straightforwardly, by applying the principles presented previously, [3]:

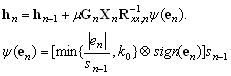(13)

where ☺ denotes elementwise multiplications and |^.| in |e_n| operates on the individual elements.

3. Investigation of Robust Parameters

This section examines the relationship and function of the robust algorithm. In the robust PAPA Ψ(e_n) is an P-by-1. The scale factor s_n uses the first element in the limiter matrix,

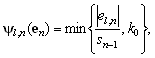(14)

(15)

 From a glance at the equations, the parameters β and λ act as a weighting on the previous scale factor values and the current error value. This relationship between the parameters and the current error value can be demonstrated through the substitution of equation (14) into (15), yielding,

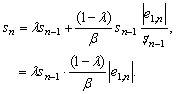(16)

 If the error is small, meaning no double talk is active; the minimum function will favour the first term and this results in following equation,

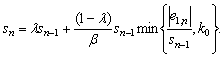(17)

From equation (17), it can be deduced that when the error is small, the algorithm uses the previous scale factor and the current error to compute the scale factor which will be used in the next iteration.
Similarly, when the error is large, the minimum function will favour the second term of equation (18) and the scale factor becomes,

(18)

In this case, the scale factor relies on the previous scale factor and k₀. This implies that when DT occurs, the scale factor will use a smaller k₀ value instead of the larger error value.

4. Simulations

The simulations were provided using MATLAB environment. The robust PAPA was simulated under user defined acoustic scenarios. The data used comprised of a real car channel (length of 2048 taps), female and male synthetic speech. 6 dB was used for DT as the ratio between the far-end speaker and the near-end speaker and a SNR of 20 dB was used for the noise as illustrated in Figure 2. The two main factors that were considered in the investigation of adaptive algorithms were rate of convergence and robustness.The misalignment (it was the main focus of this paper) is given by, ε=||h-h_ep||/||h_ep||, where h_ep is the true echo path. The scale estimate in (7), s_n , is never allowed to become smaller than 2. This inhibits bad behaviour in low noise situations.
The misalignment plot for k₀ (Fig. 3) resulted from simulations with k₀={20,1,0.7,0.5}. As it was too large, the algorithm was not restricted and a large misalignment was observed when DT occurred. This further clarified the role of k₀ as being the restricting factor in the limiter function.
Detailed investigations were carried out to find out the effects of β and λ using k₀ value found from the above. The parameters that were used during this section of the investigation are , μ=0.05, k₀=0.7, λ=0.99. For the testing of the parameter β, the misalignment plots are illustrated in Figure 4. It is demonstrated that with increasing values of β, the robustness of the algorithm increased.
Practical values of the robust parameters were best to be [0.99, 1) for λ in [3]. Clear the misalignment (Fig. 5) was considerably smaller when λ was large. None of the results for different λ values appeared to be severely affected by DT. However, the algorithm was more sensitive to changes for λ=0.94 and λ=0.96 since the plots diverge when the other two results did not. This corresponded to the expectations that a smaller value of λ would increase the weighting on the current values in the scale factor, thus producing a less robust solution.

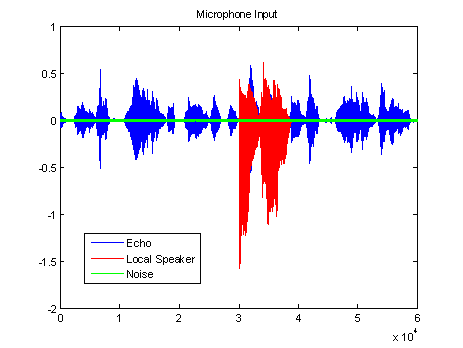
Fig. 2 Echo signal, local speaker and background noise.

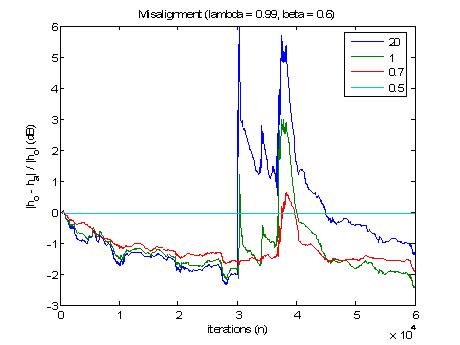
Fig. 3 Misalignment for k₀.

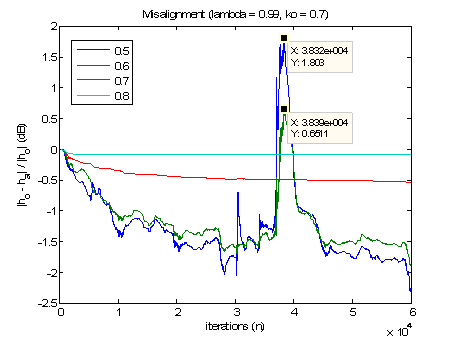
Fig. 4 Misalignment for β.

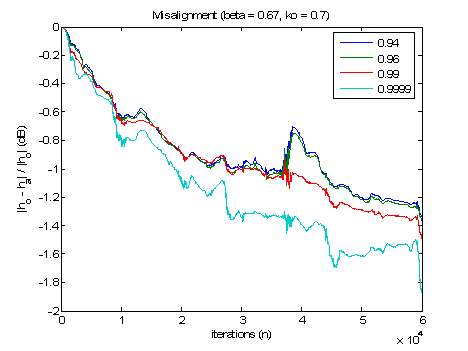
Fig. 5 Misalignment for λ.

5. Conclusion

The parameter k₀ was the main robust parameter, which affected the level of divergence in the algorithm DT occurred. This parameter was the key to the limiter function, which limits the magnitude in the filter weight adaptation. The other two robust parameters β and λ could be regarded as fine-tuning parameters, which allowed users to adjust the level of robustness integral to the robust adaptive algorithms. The recommended values suggested in ([3], [10]) were found to be relevant to the acoustic environment used in the simulations. An increase in the values of β and λ was found to increase the memory of the algorithm, meaning that the algorithm demonstrated slower convergence and reacted slower to changes in the input signal. Conversely, decreasing the values of β and λ also decreased the memory of the algorithm thus allowing it to track changes more readily, as it was less robust; the algorithm was found to diverge when double-talk occurred. It was concluded that to configure the robust adaptive echo cancellation algorithms, the required degree of robustness should be known such that one can set the correct parameters. As allowing more robustness would decrease the convergence of the algorithms, it was very important to find a balance between the two key factors.

This paper has originated thanks to the support from the Ministry of Education, Youth and Sports of Czech Republic within the project MSM6840770014.

Literature

[1] C. Breining, "Control of a hands-free telephone set", Elsevier Signal Processing, vol. 61, pp. 131-143, 1997.
[2] T. Gänsler, Benesty, J., Gay, S., Acoustic Signal Processing for Telecommunication. Massachusetts: Kluwer Academic Publishers, 2000.
[3] T. Gänsler, J. Benesty, S. Gay, and M. Sondhi, "Double-Talk Robust Fast Converging Algorithms for Network Echo Cancellation," IEEE Transactions on Speech and Audio Processing, vol. 8, pp. 656-663, 2000.
[4] D. L. Duttweiler, "Proportional Normalized Least Mean Squares Adaptation in Echo Cancellers", Lucent Bell Laboratories technical memorandum BL01771N0-961001-01TMS, 1996.
[5] S. L. Gay, "PNLMS++ for Network Echo Cancellation", Lucent Bell Laboratories technical memorandum BL011332-970527-04TM, 1997.
[6] K. Ozeki and T. Umeda, "An Adaptive Filtering Algorithm using an Orthogonal Projection to an Affine Space and its Properties", Electronics and Communications in Japan, Vol. 67-A, no. 5, 1984.
[7] S. L. Gay and S. Tavathia, "The Fast Affine Projection Algorithm", Proc. of ICASSP, pp. 3023-3026, 1995.
[8] D. L. Duttweiler, "A twelve-channel digital echo canceler", IEEE Trans. Commun., vol. 26, no. 5, pp. 647-653, May 1978.
[9] T. Gänsler, "A double-talk resistant subband echo canceller", Signal Processing, vol. 65, no. 1, pp. 89-101, Feb. 1998.
[10] T. Gänsler, Benesty, J., Gay, S., Sondhi, M., "A Robust Proportionate Affine Projection Algorithm for Network Echo Cancellation," IEEE International Conference. Acoustics, Speech and Signal Processing, pp. 793-796, 2000.
[11] J. Huo, "Subband Acoustic Echo Cancellation," Curtin University of Technology, 2004, pp. 1-128.
[12] S. G. Kratzer and D. R. Morgan, "The partial-rank algorithm for adaptive beamforming", Proc. SPIE Int. Optic. Eng., Vol. 564, pp. 9-14, 1985.