Time Precision of Navigation Systems

Satellite navigation is a type of radio navigation that use radio waves from artificial satellites in order to determine points and moving receivers location, along with their movement parameters, in any place on the Earth. The most popular system of satellite navigation is GPS (Global Positioning System).

Principle of operation
Satellite navigation system principle of operation is based on measurements of distance between four satellites and receiver, using the formula:

(1)

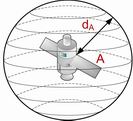
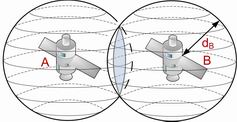
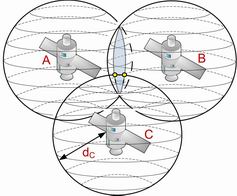
Radio waves information about local time is constantly broadcasts by each satellite; time is counted down by four cesium-beam atomic clocks. To compute the distance from satellite, GPS receiver measure time, which passed between sending and receiving the signal; difference between these two values is multiply by speed of light, which is speed of radio wave propagation. When the distance from first satellite is calculate, it is known, that the GPS receiver’s location is somewhere on sphere’s surface with satellite as a center and radius equal to the distance, Figure 1.a). By knowing distance from second satellite, it is possible to reduce this space to a circle, which is interception point of both spheres, Figure 1.b). Distance from third satellite to receiver makes possible to narrow down search area to two points, where one for being an impossible result can be rejected, Figure 1.c). In theory those data would be sufficient to determine precise distance, but the GPS receiver is equipped with quartz clocks, which are not as accurate as those very expensive atomic clocks on board of satellites with accuracy of 1 nanosecond. That is why the signal from fourth satellite is being use to synchronize quartz clock in receiver with satellite’s atomic clock [2].

a)	b)
c)
Figure 1. Positioning.

GPS radio signals
Satellite broadcast two microwave signals: C/A code and P-code.

Coarse Acquisition (C/A-code)
It is a basic signal for civil GPS receivers on the L1 frequency (1575,42 MHz), which carries navigation message and SPS code signal (Standard Positioning Service). The C/A code is a repeating 1 MHz Pseudo Random Noise (PRN) Code. L1 carrier signal is modulated by this code. The C/A code is repeated every one millisecond (1023 bits) and each satellite broadcast different PRN one, so by this they can be identify. Because C/A code is designed for civil use, it is less accurate then P-code, and it is possible to jam it (broadcast false signal to mislead the receiver about its real position). C/A code has one advantage over P-code, it is faster to gain it from satellite and compute first position.

Precision (P-code)
It is signal for the Precise Positioning Service (PPS), broadcasted on L2 frequency (1227,60 MHz). It is dedicated to be used by U.S. military because of it highly precise location information. Also it is used by PPS receivers to calculate ionospheric delays. The P-code modulates L1 and L2 carrier phase. It is a very long 10 MHz PRN code. To be free of jamming and spoofing its encrypted form is broadcasted, Y-code. To receive it a special receiver is needed, with cryptographic keys.

Navigation message
It is 50 Hz signal, which modulates L1-C/A code signal. It contains data about satellite orbit, clock corrections and other parameters.

Relativity
GPS was first technology were Einstein theory of relativity found its application. After sending first satellite, result was not as accurate as everybody expected; difference between real position and determined by GPS was more that 11 km. It became obvious that clocks on deck of satellite count time a little bit different than on earth. After first try it was necessary to provide each satellite with relativity correction. We distinguish two theories of relativity: General and Special. General Relativity (GR) predicts that clocks in a stronger gravitational field will tick at a slower rate. Special Relativity (SR) predicts that moving clocks will appear to tick slower than non-moving ones. Because Earth’s spin rate determines its shape, these two effects are not independent, and it is therefore not entirely coincidental that the effects exactly cancel. The cancellation is not general, however. The special theory, in addition to claiming, that the frequency received is a function of the relative velocity, also claims that the speed of light is isotropic relative to the (observer) receiver; what is more, the GPS system uses the earth-centered non-rotating frame and also assumes the speed of light is isotropic in that frame. The nominal velocity of a GPS satellite with respect to an earth-centered non-rotating frame is about 3,87 kilometers per second. Using this frame, the computed clock rates should slow by:

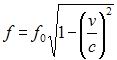(2)

where

• f is satellite clock frequency,
• f₀ is clocks on Earth frequency,
• v is speed of satellite relatively to Earth and is speed of light.

Using this expression, one obtains a frequency decrease of 8,32 parts in 10¹¹ for GPS satellites. General Relativity experiments show that the gravitational potential affects the rate at which clocks run. In order to demonstrate these effects without excessive use of mathematics, scale factor “s” was define, slightly less than one, which is used to multiply or scale the parameter of interest. This scale factor is a direct function of the gravitational potential, and can be computed from it. The lower the gravitational potential the smaller the scale factor becomes. The scale factor is defined as,

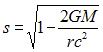(3)

where

• G is Newton's gravitational constant,
• M is the mass causing the gravitational potential,
• r is the distance from the center of the gravitational potential.

The clocks run slower (measured time appears dilated) as compared to the rate at which they would run if they were located external to the gravitational field. The comparative clock rate is given in terms of the scale factor, s, defined above as,

(4)

where

• f_s is the rate the clock would run if it were external to the gravitational potential.

There is a change in the clock frequency of the GPS satellite clocks at the time of their launch. The change in the gravitational potential at the surface of the earth to the gravitational potential at the satellite orbital height causes an increase in the average rate at which the clock runs of 5,311 parts in 10¹⁰. As stated above, the speed of the GPS satellites in orbit causes a clock frequency decrease of 8,32 parts in 10¹¹. These two effects combine to give a net increase in frequency of 4,479 parts in 10¹⁰. These two frequency-biasing effects and the additional small mean effects of the earth oblateness, sun and moon are compensated before launch by setting the frequency low by 4,45 parts in 10¹⁰ [7]. Further, each GPS receiver has built into it a microcomputer that (among other things) performs the necessary relativistic calculation when it is determining the user’s position.

Accuracy
The position accuracy is primarily dependent on the satellite position and signal delay. Several factors exist that has effect on accuracy:

Ionosphere delays
The satellite signal slows as it passes through the atmosphere. The GPS system uses a built-in model that calculates an average amount of delay to partially correct for this type of error. The ionospheric time delay is given by:

(5)

where TEC is the total number of electrons, called the Total Electron Content, along the path from the transmitter to the receiver, c is the velocity of light in meters per second, and f is the carrier frequency in Hz. TEC common definition is a number of electrons in a unit cross-section column of 1 m² area along the path and range from 10¹⁶ electrons per m² to 10¹⁹ electrons per m². This leads to the delay of 54 ns, for 1,575 GHz C/A carrier frequency for GPS satellite system and for a TEC of 10¹⁸ electrons per m². Obviously, the TEC parameter is significant for GPS system [8].

Troposphere delays
When time signal is transferred between ground stations by use of common-view satellite, one records the time of arrival of the signal and computes the time of transmission by subtracting the propagation time. By dividing the range to the satellite by the velocity of light a the propagation time is found. Nevertheless, moisture and oxygen in the troposphere have an effect on the signal velocity of propagation, which has effect on computing time of transmission and as a result, the time transfer. The geometry, the latitude, the pressure, and the temperature, all those factors has influence on this effect and may fluctuate in error from 3 ns to 300 ns. That is why a reasonable models are employed and use of high elevation angels. It should lower the differential delay between two sited to 10 ns [8].

Signal multipath
This kind of error occurs when the GPS signal is reflected off objects such as tall buildings or large rock surfaces before it reaches the receiver. This increases the travel time of the signal.

Receiver clock errors
A receiver is not provide with clock as accurate as the atomic clocks onboard the GPS satellites. For that reason, it may have very slight timing errors.

Orbital errors
Reported location of satellite, known also ephemeris, can be inaccurate, which can lead to form an error.

Number of satellites visible
The best accuracy receiver can get by seeing large number of GPS satellites. Buildings, terrain, electronic interference, or sometimes even dense foliage can block signal reception, causing position errors or possibly no position reading at all. GPS units typically will not work indoors, underwater or underground.

Satellite geometry/shading
This refers to the relative position of the satellites at any given time. Ideal satellite geometry exists when the satellites are located at wide angles relative to each other. Poor geometry results when the satellites are located in a line or in a tight grouping [3].

Conclusion
Using today’s state of the art global navigation satellite systems (GNSS), you can pinpoint your location anywhere on earth with an accuracy of less than fifteen meters. Currently, the only system available to the general public is the American Global Positioning System, which has been fully operational since mid-1994. The upcoming European competitor, Galileo, promises to improve accuracy. This made it possible to find your way through a city, solely based on the data gathered by your receiver from space. Already nowadays GNSS will find extremely useful applications, thanks to its precision in measuring the time, such as replacing seeing-eye dogs and guiding motor vehicles.

Acknowledgement
This work has been supported by the grant No. FT TA2/0475 of the Ministry of Industry and Trade of the Czech Republic.

References
[1] http://pl.wikipedia.org/wiki/Nawigacja_satelitarna, 13.03.2007
[2] LAMPARSKI J.: Navstar GPS od teorii do praktyki, Wydawnictwo Uniwersytetu Warmińsko-Mazurskiego, Olsztyn 2001
[3] NARKIEWICZ J.: GPS Globalny System Pozycyjny, Wydawnictwa Komunikacji i Łączności, Warszawa 2003
[4] www.heading.enter.net.pl/glonass.htm [22.11.2006]
[5] System nawigacyjny GALILEO. Aspekty strategiczne, naukowe i techniczne, Wydawnictwa Komunikacji i Łączności, Warszawa 2005, p. 21-36
[6] http://www.globalsecurity.org/space/world/china/beidou.htm, 13.03.2007
[7] SCHUTZ B. F.: Wstęp do ogólnej teorii względności, Wydawnictwo Naukowe PWN, Warszawa 1995
[8] Allan D.W, Weiss M.A.: Accurate time and frequency transfer during common-view of a GPS satellite, National Bureau of Standards Boulder, Colorado, 1980