|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
Témata
Doporučujeme
Kontakt
|

Vydáno dne 12. 03. 2007 (6533 přečtení) |
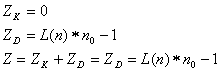 | (26, 27, 28) |
Celková konstrukční složitost kodeku je dána především potřebným počtem paměťových buněk logických operátorů. V našem konkrétním případě nemusíme uvažovat složitost a počet multiplexorů a demultiplexorů u jednotlivých zde uvedených kódů. Jelikož všechny níže uvedené kódy při shodné velikosti R používají stejný počet i konstrukci uvedených prvků. V jiných případech je tak nutné navíc počítat se složitostí slučovačů a rozdělovačů bitových posloupností nutných ke správné funkci kodéru či dekodéru.
Pro počet paměťových buněk kodéru platí:
|
| (29) |
Při výpočtu počtu paměťových buněk dekodéru lze rozdělit toto konstrukčně složitější zařízení na jednotlivé dílčí oblasti. Rozeznáváme kodér přijímače, vlastní korekce chyby a příprava korekce chyby:
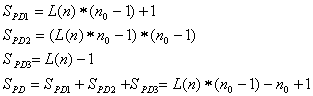 | (30, 31, 32, 33) |
Celkový počet paměťových buněk kodeku dostaneme jako součet všech dílčích částí:
|
| (34) |
Obdobně lze určit potřebný počet logických operátorů pro kodér i jednotlivé složky dekodéru, tak jako v případě paměťových buněk:
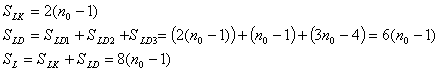 | (35, 36, 37) |
Znovu celkové zpoždění užitečné informace je způsobeno jen průchodem přes paměťové buňky v dekodéru, jelikož v kodéru slouží paměťové buňky k průběžnému tvoření zabezpečujících bitů. Pro celkové zpoždění Iwadariho kodeku při využití (11, 12) z předchozího dílu po dosazení a roznásobení platí vztahy:
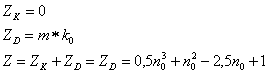 | (38, 39, 40) |
Při celkové konstrukční složitosti se snažíme využít znalosti rozměrů blokové matice B0 stejně jako u Hagelbargerova kódu. Pro počet paměťových buněk kodéru platí:
|
| (41) |
Paměťové buňky jsou u dekodéru využity pouze u kodéru přijímače a přípravy korekce. K vlastní korekci dochází přímo v bloku kodéru přijímače, kde jsou zavedeny další logické operátory a není třeba dalších paměťových buněk. Získáme při využití (11, 12) z předchozího dílu následující vztahy:
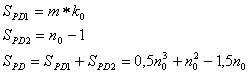 | (42, 43, 44) |
Pro celkový počet paměťových buněk kodeku dostaneme:
|
| (45) |
Logické operátory jsou použity v kodéru i ve všech jednotlivých částech dekodéru - kodér přijímače, vlastní korekce chyby a příprava korekce chyby. Pak pro množství potřebných logických operátorů platí:
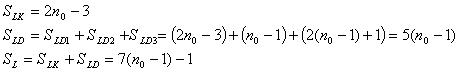 | (46, 47, 48) |
Celkové zpoždění je způsobeno jen průchodem informačních bitů přes jednu větev paralelního větvení paměťových buněk v dekodéru, jež slouží k odvození zabezpečujícího bitu na straně příjemce. Pro Berlekamp-Preparatův kodek dostaneme:
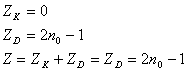 | (49, 50, 51) |
Jako v dřívějších případech se využije znalosti rozměrů blokové matice B0 pro stanovení konstrukční složitosti. Počet paměťových buněk kodéru je určen vztahem:
|
| (52) |
Paměťové buňky jsou u dekodéru využity pouze u kodéru přijímače a přípravy korekce. Opět dochází k opravě přímo v bloku kodéru přijímače, kde za tímto účelem jsou vytvořeny další vazby a platí:
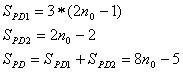 | (53, 54, 55) |
Celkový počet paměťových buněk kodeku je dán součtem všech dílčích částí:
|
| (56) |
Logické operátory jsou využity u kodéru, ovšem u dekodéru jen v blocích přípravy korekce chyby a korekce chyby. Z kodéru přijímače na straně příjemce jsou potřebná data počítána přímo v oblasti přípravy korekce. Potřebný počet logických operátorů je dán:
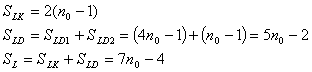 | (57, 58, 59) |
Byly uvedeny všechny potřebné vztahy, jež slouží jako výběrová kritéria při optimalizaci. Nyní si jednotlivé varianty různých kódů porovnáme. Potřebný ochranný interval určíme ze vztahů (5, 14, 22), zpoždění způsobené průchodem informace kodekem přes paměťové buňky je dána (28, 40, 51). Tyto parametry určují především kvalitu daného kodeku. Pomocí dalších parametrů lze posuzovat jeho složitost. Počet nutných paměťových buněk je dán (34, 45, 56). K zajištění zabezpečení je samozřejmě třeba provést jisté matematické operace, k čemuž slouží logické operátory a pro jejich počet platí (37, 48, 59).
Přehledně všechny vlastnosti prezentovaných konvolučních kódů jsou uvedeny v Tab. 1. Zde navržené systémy mají stejný informační poměr R a maximální opravitelnou délku shluku chyb b. Z tabulky je zřejmé, že při stejné informační rychlosti a velikosti opravitelné chyby má sledované veličiny nejnižší (a tím pádem nejlepší vlastnosti) Berlekamp-Preparatův kód. Vyžaduje nejkratší ochranný interval má nejkratší zpoždění přenášené zprávy průchodem paměťových buněk a k realizaci kódu je třeba nejmenší počet paměťových buněk. Navíc na rozdíl od Hagelbargerova kódu nemůže u Berlekamp-Preparatova a Iwadari-Maseryova kódu nastat nekonečné šíření chyby.
| Kód | A [bit] | Z [bit] | SP | SL |
| Hagelbargerův | 47 | 11 | 55 | 24 |
| Iwadari-Maseryův | 51 | 39 | 81 | 20 |
| Berlekamp-Preparatův | 28 | 7 | 34 | 24 |
Tab. 1 - Kódy s hodnotami sledovaných vlastností pro konečný výběr nejvhodnější varianty
Výše popsaný způsob pracuje s kódovým zabezpečením v podstatně širších souvislostech. Neomezuje se pouze na zabezpečovací kód a všímá si dalších vlastností, které jsou důležité pro výběr optimální varianty při realizaci.
Dnes se již standardně a zcela systematicky používají při přenosu zpráv v digitálních sítích bezpečnostní kódy. Přenos signálů v digitální formě umožňuje značně rozšířit nabídku poskytovaných služeb a dosáhnout kompatibility s jinými digitálními sítěmi, a to nejen v rámci jednoho státu, ale po celém světě. U konvolučních kodů se vkládá do signálu přídavná redundance tím, že se nad původním a zpožděným bitovým tokem provádí podle známých pravidel jisté matematické operace. Tato výpočetní náročnost klade vyšší nároky na procesorový výkon. Kódování a dekódování je proto v komunikačních systémech většinou zajišťováno na signálových procesorech DSP. Vysoký výpočetní výkon tyto procesory předurčuje i pro velmi náročné aplikace, které požadují řízení v reálném čase, což používání zabezpečovacích kódů vyžaduje.
Existuje velké množství různorodých metod zabývajících se použitím a nalezením co nejvhodnějšího zabezpečovacího kódu. V dnešní době je velmi důležité najít co nejvhodnější řešení, které se liší podle nároků na něj kladených, jelikož zabezpečení dosahujeme zvýšením nadbytečnosti na úkor vlastního přenosu informace. Záleží především na reálných podmínkách přenosu od vysílače k přijímači zabezpečované informace. Zabezpečení přenášené informace nepřetržitým způsobem jsme schopni realizovat pomocí konvolučních kódů. Nejvíce se využívají ty kódy z této skupiny, které zajišťují ochranu před shlukovými chybami různé délky. Proti blokovým kódům představuje značnou výhodu daleko menší potřeba rozrůstání kódu (redundance) z důvodu zajištění zabezpečení zprávy. Avšak je nutné mezi shluky chyb pro korektní opravu zachovat určitý ochranný interval, ve kterém nesmí dojít během přenosu k chybě.
Tento článek vznikl za podpory výzkumného projektu FRVŠ - 993 G1 "Simulace zabezpečovacích korekčních kódů a její začlenění do výuky předmětu Datová komunikace"
[1] Křivánek, V., Číka, P.: Simulace shlukových chyb v Matlabu. Elektrorevue, 2006, č. 35, str. 1-10. ISSN 1213-1539.
[2] Křivánek, V.: Verification of the Error-Control Security Process by Means of Simulation. International Transactions
on Communication and Signal Processing, 2006, vol. 9, no. 1, p. 128-136, ISSN: 1738-9682.
[3] Němec, K.: Kódové zabezpečovací systémy. Teze habilitační práce, ÚTKO FEI VUT Brno, Brno 1999, 34s.,
ISBN 80-214-1312-3.
[4] Němec, K.: Výběr optimálního protichybového kódu. Elektrorevue, 2006, č. 54., str. 1-9. ISSN 1213-1539.
[5] Shu, L.; Costello, D.: Error Control Coding – Fundamentals and Applications. Prentice-Hall, Inc., Englewood Cliffs,
New Jersey 1983, 603 p., ISBN 0-13-283796-X.
Tento web site byl vytvořen prostřednictvím phpRS - redakčního systému napsaného v PHP jazyce.
Na této stránce použité názvy programových produktů, firem apod. mohou být ochrannými známkami
nebo registrovanými ochrannými známkami příslušných vlastníků.