|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
Témata
Doporučujeme
Kontakt
|

Vydáno dne 27. 11. 2009 (5348 přečtení) |
|
| (1) |
kde reálná odezva o n proměnných
Volterrovy filtry patří do třídy nelineárních nerekurzivních polynomiálních filtrů [1], [2] kombinující filtry založené na rozvoji do Taylorovy řady a lineární filtry. Polynomiální filtr bez paměti reprezentovaný Taylorovou řadou lze použít např. pro modelování systémů s obecnou saturační charakteristikou [2]. Základní myšlenka Volterrova filtru vychází z definování mnoha navzájem nezávislých bloků s jedinečnou n-rozměrnou odezvou reagující na danou kombinaci vstupního signálu. Toto lze vyjádřit
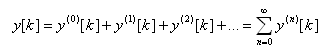 | (2) |
kde
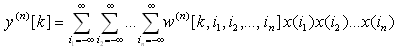 | (3) |
kde
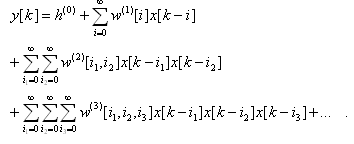 | (4) |
Pro další zjednodušení budeme předpokládat symetrii koeficientů odezvy systému,
|
| (5) |
|
| (6) |
Dalším předpokladem je omezení délky odezev jednotlivých komponent hodnotou
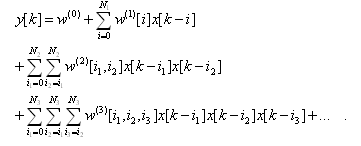 | (7) |
V další úvaze se omezíme na Volterrův filtr druhého řádu s vynecháním nulté komponenty a délkou odezvy systému pro oba bloky rovnou
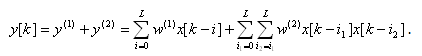 | (8) |
V kmitočtové oblasti bude obecně pro složku
|
| (9) |
Převod kvadratické složky
 |
Obrázek 1: a) Blokové schéma kvadratické komponenty Volterrova filtru pro délku odezvy L(2) = 5 v kmitočtové oblasti,
b) Rozložení koeficientů odezvy kvadratické složky filtru pro délku odezvy L(2) = 5 a zobrazení patřičného buzení.
Na obr. 1a) je zobrazeno blokové schéma kvadratické komponenty Volterrova filtru pracujícím v kmitočtové oblasti s délkou odezvy systému
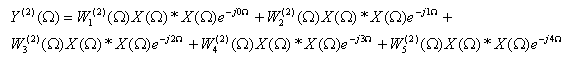 | (10) |
kde * představuje operaci cyklické konvoluce.
Filtry FLMS [4] využívají pro výpočet v kmitočtové oblasti konvolučních nebo korelačních technik označovaných v anglosaské literatuře jako “overlap-save” nebo “overlap-add” [3], [4]. Ve většině případů tvoří systém filtr s délkou impulsové odezvy danou velikostí zpracovávaného bloku vstupních dat. Takový to „dlouhý“ filtr má nevýhodné vlastnosti z hlediska citlivosti na kvantování výpočtů, rychlosti konvergence a stability systému [2]. Vylepšení rychlosti konvergence a stability přinášejí filtry MDF [3] pracujícími s mnoha krátkými lineárními filtry spojenými do jednoho bloku požadované délky impulsové odezvy. Každý filtr je v daném subbloku řízen adaptivně na daném úseku výsledné impulsové odezvy. Výsledná délka impulsové odezvy Lje daná součtem délek dílčích filtrů. Celkový počet zpožděných bloků v kaskádě je označen symbolem M. Pak pro délku FFT označenou N platí 2L/M. Hodnoty L,M volíme tak, aby byla délka filtru v daném subbloku celočíselná a měla výhodnou délku z hlediska výpočtu FFT. V prvním kroku je vstupní signál rin převeden do kmitočtové oblasti pomocí FFT
|
| (11) |
Převod (11) je proveden pouze v tomto prvním kroku a do následujících bloků je dále jen překopírováván. Ostatní kombinace vstupního signálu jako např. kvadrát či jinak posunuté násobení v kvadratické složce filtru je prováděno pouze v kmitočtové oblasti. Pro výstupní chybový signál platí
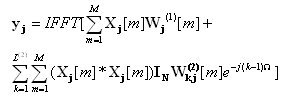 | (12) |
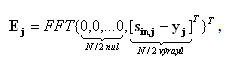 | (13) |
kde W[m,j] je vektor koeficientů odezvy, yj uvedené ve vztahu (13) je omezeno na délku (N/2,N> a Sin,j představuje signál po průchodu rušivou soustavou v časovém okamžiku j. Z LMS kritéria pro výpočet korekce váhovacích koeficientů odezvy Volterrova filtru platí
|
| (14) |
|
| (15) |
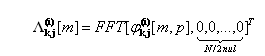 | (16) |
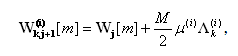 | (17) |
kde
 |
Obrázek 2: a) Blokové schéma adaptivního Volterrova filtru realizovaného pomocí mnoha krátkých zpožděných bloků v kmitočtové oblasti, kde S/P je sériově paralelní a P/S je paralelně sériový převodník, b) Obecné schéma systému pro potlačování akustické ozvěny v telekomunikační technice, c) Proměnné vstupující/vystupující do/z jednotlivých adaptivních bloků.
Každý Volterrův filtr z blokového schématu na obr. 2a představuje výpočet jednoho sloupce koeficientů kvadratické odezvy systému zobrazené na obr. 3. První filtr představuje výpočet koeficientů pro kombinace bloků (MxM, Mx(M-1), ..., Mx1), druhý filtr pro kombinace ((M-1)x(M-1), (M-1)x(M-2), ..., (M-1)x1), atd. Celkový počet bloků potřebných pro výpočet všech koeficientů odezvy systému je
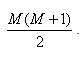 | (18) |
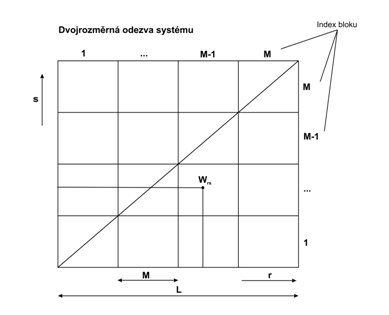 |
Obrázek 3: Rozdělení dvojrozměrné odezvy Volterrova filtru na jednotlivé subbloky a jejich indexace. Délka odezvy systému je označena symbolem L, délka subbloku M. Indexy r a s jednoznačně určují daný koeficient odezvy systému W.
V simulaci je porovnávána výše navržená bloková struktura filtru pracujícím v kmitočtové oblasti s délkou odezvy systému L=128 a M=24 se stejným filtrem pro L=128 a M=24. Vstupní signál má vlastnosti normálního rozdělení se směrodatnou odchylkou
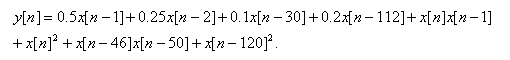 | (19) |
Rovnici rušivé soustavy lze zvolit libovolně při dodržení podmínky celkové délky odezvy systému a použitím nejvýše kvadratických členů. Pro výpočet výsledných konvergenčních charakteristik je použit algoritmus používající normalizovanou střední kvadratickou odchylky pruměrovanou přes deset nezávislých měření v dB danou
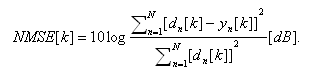 | (20) |
Na obr. 4 jsou zobrazeny konvergenční charakteristiky daných adaptivních filtrů. Při použití kratšího bloku je patrná rychlejší konvergence výsledného filtru, kterou zajišťuje koeficient M/2 (násobící konstanta) v rovnici (17). Při použití stejné hodnoty násobící konstanty vypočtené s použitím krátkých filtrů pro dlouhé filtry bude tato adaptivní soustava vykazovat vysokou míru divergence. Násobící konstanta M/2 byla stanovena experimentálně za použití simulací pro normální rozdělení vstupního signálu se směrodatnou odchylkou
 |
Obrázek 4: Konvergenční charakteristika výsledného adaptivního filtru popsaného na obr. 2a pro různý počet vnitřních bloků.
Použití Volterrova filtru druhého řádu v kmitočtové oblasti přináší nové možnosti při potlačování akustické ozvěny v telekomunikacích. Kvadratická komponenta sleduje další nelineární vazby rušivé soustavy, které dokáže lépe aproximovat a tedy i lépe potlačit. Použití blokové struktury přináší zlepšení rychlosti konvergence a zvýšení stability celé soustavy v důsledku použití kratších filtrů. Krátké vstupní bloky také snižují velikost zpoždění danou S/P převodníkem na vstupu soustavy. Další krok bude zaměřen na zjednodušení výpočtu aktualizace jednotlivých koeficientů odezvy Volterrova filtru. Tato výpočetní náročnost roste exponenciálně s délkami filtrů v jednotlivých složkách a s počtem těchto složek.
Tato práce byla podpořena výzkumným záměrem Výzkum perspektivních informačních a komunikačních technologií MSM6840770014.
[1] A. Borys, “Discrete Volterra Series and Nonlinear Echo Cancellation”, Book, CRC Press LLC, London, 2001.
[2] F. Kuch, “Adaptive Polynomial Filters and their Application to Nonlinear Acoustic Echo Cancellation”, Doktor-Ingenieur, Der Technischen Fakultat der Friedrich-Alexander-Universitat Erlangen-Nurumberg zur Erlangung des Grades, Erlangen, 2005.
[3] J. Sien, K.K. Pang, “Multidelay Block Frequency Domain Adaptive Filter”, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 38, pp. 373-376, No. 2, February 1990.
[4] J.J. Shynk, “Frequency-Domain and Multirate Adaptive Filtering”, IEEE SP MAGAZINE, pp. 1-37, January, 1992.
[5] M. Zeller, W. Kellermann, “Fast Adaptation of Frequency-domain Volterra Filters Using Inherent Recursions of Iterated Coefficient Updates”, University of Erlangen-Nuernberg, EURASIP, 2007.
[6] F. Kuech, W. Kellermann, Member, IEEE, “Partioned Block Frequency- Domain Adaptive Second-ord Volterra Filter”, IEEE Transactions on Signal Processing, Vol. 53, No. 2, February 2005.
[7] J. Uhlíř, P. Sovka, “Číslicové zpracování signálů”, Vydavatelství ČVUT, Praha 2002, ISBN 80-01-02613-2.
Tento web site byl vytvořen prostřednictvím phpRS - redakčního systému napsaného v PHP jazyce.
Na této stránce použité názvy programových produktů, firem apod. mohou být ochrannými známkami
nebo registrovanými ochrannými známkami příslušných vlastníků.