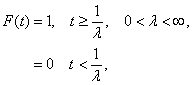Pro stručné a přehledné vyjádření typu obsluhového systému v teorii hromadné obsluhy se vžilo použití Kendallovy klasifikace. Cílem tohoto článku je seznámit čtenáře se základním členěním obsluhových systémů a použitím Kendallova značení.
Kendall classification of service systems
Abstract
To present service system in waiting-line theory in a short and general way the Kendall classification is used. Purpose of this paper is to show to the reader basic segmentation of service system and signification of Kendall use.
Popis obsluhového systému
Pod pojmem systém hromadné obsluhy1 nebo též zkráceně obsluhový systém (OS) si můžeme představit jakýkoliv systém
zajišťující obsluhu požadavků (zákazníků), jež obsluhu po systému požadují. Obsluhové systémy jsou součástí našeho každodenního života aniž si
to vlastně uvědomujeme. Například pokud někde čekáme (na vlak, u pokladny na lístek do kina, u lékaře) jsme vlastně zákazníkem (požadavkem) daného obsluhového systému.
Systémy hromadné obsluhy samozřejmě nalezneme i v telekomunikacích, kde se například používají pro dimenzování svazků, spojovacích polí, řídících prvků ...
Obr. 1 Schéma jednoduchého obsluhového systému
Schéma jednoduchého obsluhového systému je znázorněno na obr 1. Pro popis obsluhových systému se používá model skládající se z:
- N obsluhových linek (serverů) určených k obsluze požadavků přicházejících z S zdrojů,
- R míst určených k čekání požadavků,
- řízení obsluhového systému (formálně uvedeno pro úplnost).
Požadavky, které systém obsluhuje, vznikají ve zdrojích a přicházejí jako tzv. vstupní tok do obsluhového systému.
Při vstupu požadavku do systému, je řízením OS rozhodnuto, bude-li požadavek systémem obsloužen, nebo bude odmítnut.
Při přijetí požadavku do systému je buď přímo započata obsluha daného požadavku (pokud je volná obsluhová linka), nebo požadavek čeká na obsluhu.
Po skončení obsluhy požadavek opouští obsluhový systém a stává se součástí výstupního toku obsloužených požadavků.
Kendallova klasifikace
Je tomu již přes padesát let od doby, kdy David George Kendall
publikoval [1] své značení OS:
význam jednotlivých písmen je uveden v tab.1.
Tab.1: Význam písmen Kendallova značení
| písmeno |
popis |
| A |
distribuční funkce intervalů mezi příchody |
| B |
distribuční funkce doby obsluhy |
| N |
počet obsluhových linek (přirozené číslo nebo symbol ∞) |
Původní Kendallovo značení (1) ponechává neurčeny další důležité charakteristiky systému jakými jsou:
maximální počet čekajících (délka fronty), způsob výběru zákazníků z fronty, atd. O tyto údaje bylo postupně původní Kendallovo
značení rozšířeno [3]:
| A / B / N / K / S / X |
(2) |
význam prvních tří písmen zůstává shodný s původním Kendallovým značením (tab. 1) a význam rozšiřujících písmen je uveden v tab. 2.
Tab.2: Význam písmen rozšiřujících původní Kendallovo značení
| písmeno |
popis |
| K | maximální počet požadavků v systému (počet obsluhových linek plus počet míst pro čekající , K=N+R) nebo pouze počet míst pro čekající (K=R) |
| S | počet zdrojů požadavků (zákazníků), neuvádí se pokud je nekonečný |
| X | režim fronty: FCFS (First Come - First Served), FIFO (First In - First Out), FCLS (First Come - Last Served), LIFO (Last In - Last Out), SIRO (Service In Random Order), RAND(Random) |
Je nutné upozornit na jistou nejednoznačnost použití čtvrtého písmene K.
Autoři na tomto místě uvádějí buď maximální počet požadavků v systému (K=N+R) nebo jen počet míst pro čekající požadavky.
Na pozicích písmen A a B se vžilo použití následujících písmen značících danou distribuční funkci intervalů mezi jednotlivými příchody (pro A)
nebo distribuční funkci doby obsluhy (pro B):
| M | ~ | Exponenciální rozložení intervalů mezi příchody, (doby obsluhy) |
| D | ~ | Deterministické (konstantní intervaly mezi příchody nebo konstantní doba obsluhy) |
| Ek | ~ | Erlangovo rozložení k-tého řádu (E1=M) |
| Hk | ~ | Hyperexponenciální rozložení k-tého řádu |
| Kn | ~ | rozložení s n stupni volnosti |
| GI | ~ | nezávislé příchody (General Independent) |
| G | ~ | obecné (General), tj. jakékoliv rozložení |
| GMPP | ~ | Generally Modulated Poisson Process: - poissonovský proces s proměnnou intenzitou |
| MMPP | ~ | Markov Modulated Poisson Process (Markovovsky modulovaný poissonovský proces): - speciální případ GMPP (intenzita se mění (moduluje) Markovovským řetězcem) |
| SPP | ~ | Switched Poisson Process (přepínaný poissonovský proces): - jde o dva vzájemně se střídající poissonovské procesy (M) |
| IPP | ~ | Interrupted Poisson Process (přerušovaný poissonovský proces): - speciální případ SPP, kde intenzita jednoho z toků je nulová |
Pro dimenzování telekomunikačních sítí založených na spojování okruhů se nejčastěji používá Markovovský model M/M/N/0. Avšak s postupným rozvojem nových telekomunikačních služeb (převážně multimediálních) se začal významně měnit i charakter vstupních toků nabízených těmto systémům a také charakter doby obsluhy. Tato výrazná změna vedla k tvorbě nových modelů [4]. Mezi dnes nejpoužívanější patří MMPP/M/N/0, IPP/M/N/0.
Dalším významným milníkem v teorii hromadné obsluhy bylo zavedení systémů pracujících s diskrétním časem (ve všech doposud uvedených rozloženích je čas uvažován jako spojitý). Pro systémy tohoto typu se začaly vyvíjet nové modely [4] :
| GEOM | ~ | geometrické rozložení: - Bernoulliho proces |
| GMDP | ~ | Generally Modulated Deterministic Process: - determinstický proces s proměnnou intenzitou |
| MMDP | ~ | Markov Modulated Deterministic Process (Markovovsky modulovaný deterministický proces): - speciální případ GMDP (změna intenzity je určena Markovovským řetězcem) |
| SDP | ~ | Switched Deterministic Process (přepínaný deterministický proces) |
| IDP | ~ | Interrupted Deterministic Process (přerušovaný deterministický proces) |
| SBBP | ~ | Switched Batch Bernoulli Process: - zvláštní případ Bernoulliho procesu se skupinovými příchody [5] |
Pozn.: V případě prioritních toků nebo priorit v obsluze se lze setkat s označením
® nad daným písmenem.
Příklady použití Kendallova značení
- M / M / N / 0 - jde o Erlangův model:
- exponenciální rozložení intervalů mezi příchody (systém s poissonovským vstupním tokem),
- exponenciálně rozdělená doba obsluhy,
- N obsluhových linek,
- počet míst pro čekající R=0, OS se ztrátou (bez možnosti čekání).
- H2 / D / 1 / ∞
- hyperexponenciální rozložení intervalů mezi příchody (druhého řádu),
- doba obsluhy je konstantní (neměnná pro všechny požadavky),
- systém má jednu obsluhovou linku pro obsluhu přicházejících požadavků,
- délka fronty není omezena,
- vzhledem k tomu, že není uveden režim fronty, implicitně se předpokládá režim fronty FIFO.
- M+M / D+Ek / N / 0
- vstupní tok se skládá z dvou rozdílných (nezávislých) vstupních toků typu M (každý má jinou intenzitu λ),
- doba obsluhy požadavků prvního vstupního toku je konstantní a doba obsluhy požadavků druhého vstupního toku má Erlangovo rozložení k-tého řádu,
- systém má N obsluhových linek,
- příchozím požadavkům není dovoleno čekat na obsluhu, pokud nejsou přímo vzaty do obsluhy, jsou systémem odmítnuty (systém se ztrátami).
Popis nejčastěji používaných rozložení
Pro distribuční funkce F, hustoty pravděpodobnosti f, střední hodnoty E a rozptyly D platí následující vztahy:
- Exponenciální rozložení (M):
- distribuční funkce:
- hustota pravděpodobnosti:
- střední hodnota a rozptyl:
- Rozložení s pravidelnými (deterministickými) příchody (D):
- distribuční funkce:
- frekvenční funkce:
- střední hodnota a rozptyl:
- Erlangovo rozložení k-tého řádu (Ek):
- distribuční funkce:
- hustota pravděpodobnosti:
- střední hodnota a rozptyl:
- Hyperexponenciální rozložení k-tého řádu (Hk):
- distribuční funkce:
- hustota pravděpodobnosti:
- střední hodnota a rozptyl:
Distribuční funkce a hustoty pravděpodobnosti výše uvedených rozložení jsou zobrazeny na obrázcích č. 2 a 3.
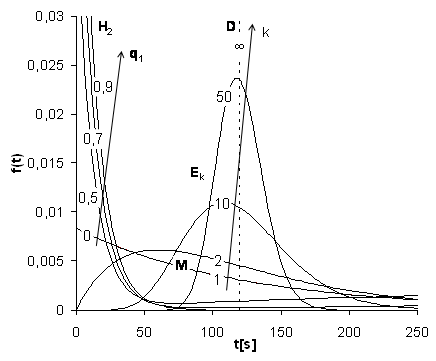
Obr. 2 Hustoty rozložení f(t) M, Ek, D a Hk pro E(t) = 120 s
Obr. 3 Distribuční funkce F(t) rozložení M, Ek, D a Hk pro E(t) = 120 s
Z obr. 2 a 3 je zřejmé, že exponenciální rozložení tvoří „hranici“ mezi hyperexponenciálním a Erlangovým rozložením. Rozložení s pravidelnými příchody je limitním případem Erlangova rozložení k-tého řádu pro k®∞, při konstantní střední hodnotě.
Závěr
Cílem článku bylo seznámit čtenáře s Kendallovou klasifikací a podat přehledný návod k použití Kendalova značení.
Další vývoj v oblasti teorie hromadné obsluhy si sice vyžádal rozšíření o další prvky značení (K, S, X) oproti původnímu Kendallovu návrhu.
Přesto však je nutné zdůraznit, že pravě David George Kendall se svým uceleným pohledem na třídění OS,
významnou měrou přispěl k zjednodušení zápisu a zpřehlednění dělení různých typů systému hromadné obsluhy.
Tento příspěvek vznikl za podpory grantu FRVŠ "Dimenzování obsluhového systému pro multimediální služby" č.: 2477/2005 a v rámci projektu NPV 1ET300750402.
Literatura a odkazy
[1] Kendall, D. G. Stochastic processes occurring in the theory of queues and their analysis by the method of the imbedded Markov chain. In The Annals of Mathematical Statistics Vol.24, 1953, s. 338–354.
[2] Biography - from St.Andrews University [online]. 1998 [cit. 2005-11-16]. Dostupný z WWW: <http://www-history.mcs.st-andrews.ac.uk/Mathematicians/Kendall.html>.
[3] ITC, ITU-D SG2. Handbook “TELETRAFFIC ENGINEERING”. 2005. 350 s. Dostupný z WWW: <http://oldwww.com.dtu.dk/teletraffic/handbook.html>.
[4] ROBERTAZZI, T. G. Computer Network and Systems: Queueing Theory and Performance Evaluation. 3rd edition. Springer, 2000. 410 s. ISBN 0-387-95037-0.
[5] HASHIDA, O., TAKAHASHI, Y., SHIMOGAWA, S. Switched Batch Bernoulli Process(SBBP) and the Discrete-Time SBBP/G/1 Queue with Application to Statistical Multiplexer Performance. In IEEE Journal on Selected Areas in Communicatins. 1991. ISSN 0733-8716 .
[6] Bibliografické citace [online]. 2004-2005 [cit. 2005-11-16]. Dostupný z WWW: <http://www.citace.com/>.
1 Systém hromadné obsluhy poskytuje obsluhu většímu počtu zákazníků, nejde tedy o jednorázové posloužení jednotlivci.