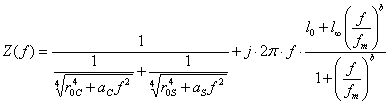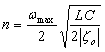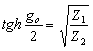Umělé vedení je elektrický nebo elektronický obvod, který se svými přenosovými vlastnostmi co možná nejvíce blíží vlastnostem skutečného vedení. Předmětem tohoto příspěvku je rozbor známých návrhových metod a vlastností umělých vedení.
Artificial Transmission Lines in Telecommunication Technique
Abstract
An artificial transmission line is a four-terminal electrical network (i.e. an electrical circuit) that has transmission characteristics of a real transmission line and therefore can be used to simulate it. The general aim of this article is to examine and describe ancient design methods and basic characteristics of the artificial transmission lines.
Úvod
Na účastnické vedení se můžeme dívat jako na přenosové médium pro telekomunikační systém a jeho vlastnosti při šíření signálu jsou plně charakterizovány teorií přenosových vedení. Pro charakterizování přenosových vedení lze použít dva různé přístupy. Pokud je cílem vyšetření elektrického a magnetického pole, lze pro analýzu přenosového vedení využít tří-dimenzionální elektromagnetické veličiny. V tomto případě nazýváme přenosové vedení vlnovodem a pro jeho analýzu použijeme Maxwellovy rovnice. Pokud je však cílem rozbor šíření signálu či energie, zjednoduší se náš popis na jedno-dimenzionální matematický model tj. přenosové vedení. Přenosové vedení lze tedy zkoumat na základě teorie obvodů, kde pracujeme s proudem a napětím namísto zmiňovaných proměnných elektromagnetického pole. Přenosové vedení se v různých variantách vyskytují v nejrůznějších aplikacích, avšak, bez ohledu na typ, délku, či konstrukci pracují všechny na stejných principech.
Účastnická vedení v přístupové části telekomunikační sítě původně sloužila pouze pro přenos telefonního hovorového signálu v pásmu 300 Hz až 3,4 kHz. V dnešní době jsou však používána pro stále vyšší a vyšší kmitočtová pásma, digitální účastnické přípojky DSL (Digital Subscriber Line) využívají frekvenční pásmo v řádech MHz. Tuto skutečnost je třeba brát v úvahu i při návrhu umělých vedení. S ohledem na tyto a další počáteční požadavky byly prozkoumány známé metody návrhu umělých vedení, jež jsou popsány v průběhu tohoto článku, a byla také vytvořena metoda experimentální, jejíž rozbor je proveden v navazujícím článku Modul umělého vedení pro digitální účastnické přípojky.
Základní vlastnosti symetrických párů
Přenosové vedení je obvodem s rozprostřenými parametry, tj. jeho obvodové veličiny jsou kromě času také funkcemi prostorových souřadnic a probíhající děje mají vlnový charakter. Elektrické vlastnosti symetrických párů jsou definovány s využitím klasického modelu přenosového vedení. Přijmeme-li předpoklad, že vedení je homogenní (vedení s konstantním průměrem a zkrutem po celé jeho délce), tj. uvedené diferenciální parametry jsou po celé délce vedení konstantní, můžeme zavést primární parametry – R, L, C a G jakožto veličiny měrné. Tyto parametry jsou závislé na frekvenci, teplotě a vlhkosti. Pro většinu simulací či modelů je vliv frekvence zásadní. Vliv frekvence má za následek různé hodnoty těchto parametrů pro různé frekvence. Obr. 1 zobrazuje grafické vyjádření jednoho segmentu přenosového vedení délky ε.
Obr. 1 Ekvivalentní obvod přenosového vedení
Primární parametry vedení mohou být použity k výpočtu sekundárních parametrů vedení, jedná se o charakteristickou impedanci Z0 a měrnou míru přenosu γ, kde reálnou a imaginární částí měrné míry přenosu jsou funkce útlumu α [Np/km resp. dB/km] a fázového posuvu (zkreslení) β [rad/km].
Umělá vedení
Čtyřpóly, které napodobují přenosové a impedanční charakteristiky homogenních vedení, se nazývají umělými vedeními (UV). V telekomunikační technice je umělé vedení elektrický obvod, který má parametry jako je charakteristická impedance, fázový posuv a další, stejné jako skutečné vedení, a proto může být použit pro modelování skutečného vedení v jednom či více ohledech. Požadavky jsou většinou specifikovány pro určitý frekvenční rozsah. V podstatě se tedy jedná o realizaci přenosového čtyřpólu s danými frekvenčními charakteristikami.
Přenosové vedení je systém s rozprostřenými parametry, avšak pro pochopení vlastností šíření vln, je lepší si přenosové vedení představit jako sériové spojení systémů se soustředěnými parametry. To jsou systémy jejichž velikost je nulová, takže přenos vlny skrze takovýto systém trvá nulový čas. Za nejjednodušší reprezentaci přenosového vedení můžeme považovat samotnou impedanci. Koncept vedení složeného z nekonečně malých elementů indukčnosti, odporu, kapacity a svodu může být použit pro získání diferenciálních rovnic. Tato jednoduchá reprezentace skutečného vedení je dostatečná, avšak ne zcela přesná. Vedení musí být pro nejvyšší uvažované frekvence vstupního signálu tzv. elektricky krátké tj. l << λ, pak můžeme pro danou frekvenci soustředit rozprostřené parametry a získat soustředěný ekvivalentní obvod symetrického páru vedení. Za účelem zvýšení frekvenčního pásma modelů se soustředěnými parametry, lze provést rozdělení vedení do několika elektricky krátkých sekcí a modelování každé z nich aproximačním modelem se soustředěnými parametry. Analýza tohoto přístupu však ukázala, že zisk z rozšíření frekvenčního pásma není až tak veliký a modelování vedení pomocí velkého počtu např. T modelů se soustředěnými parametry nevede k požadovaným výsledkům. Nicméně mohou být tyto modely použity pro analýzu vedení jak v časové, tak ve frekvenční oblasti. V minulosti se k návrhu umělých vedení nejčastěji využívali dvě návrhové metody:
- modelování vlastností vedení délky l kaskádou n stejných čtyřpólů se soustředěnými parametry,
- modelování vlastností vedení délky l jediným čtyřpólem se soustředěnými parametry.
Ve zvoleném frekvenčním pásmu se u skutečného vedení výrazně projevuje frekvenční závislost primárních parametrů, které je možno korektně modelovat např. jedním z modelů společnosti British Telecom. Volba modelu závisí zejména na pracovním frekvenčním pásmu a zvolené přesnosti modelování. Pro složitost modelu se pro jeho numerické vyjádření jednotlivých výpočtů využívá výpočetní techniky (Matlab). V našem případě využijeme třinácti parametrový model primárních parametrů. Zjednodušený postup návrhu umělého vedení lze pro všechny uvažované metody návrhu shrnout následovně:
- Volba konkrétního typu vedení spolu s určením konstant potřebných pro numerické vyjádření modelu primárních parametrů. Potřebné konstanty jsou, pro širokou škálu typů vedení, uvedeny v doporučení ITU-T G.996.1 v Tab. 7.
- Určení požadovaných vlastností vedení pro danou metodu (impedance naprázdno, nakrátko, charakteristická impedance, měrný útlum apod.), výpočty budou realizovány v prostředí Matlab.
- Pomocí vhodné numerické metody se budeme snažit nalézt parametry obvodu podle použité metody tak, aby vykazoval vlastnosti, které se nejvíce blíží těm, které byly vypočteny z modelu BT#1. Numerická metoda a výpočty spojené s nalezením obvodových parametrů jsou také řešeny v prostředí Matlab.
Modelování pomocí kaskády n čtyřpólů
Tato metoda návrhu umělého vedení vychází z představy „náhradního zapojení“ elementární délky homogenního vedení, které je uvedeno na Obr. 1. Předpokládáme, že ekvivalent homogenního vedení délky l je sestaven z n stejných T článků podle Obr. 2.
Obr. 2 Náhradní zapojení homogenního vedení délky l = 1/n (km)
Při návrhu umělého vedení je třeba sledovat dvě hlavní hlediska:
- potřebný počet segmentů pro dosažení požadované přesnosti,
- frekvenční závislost primárních parametrů, která se musí projevit v konstrukci každého segmentu.
Obvodové prvky zastupující poměrnou část hodnoty primárního parametru musí být nahrazeny náhradním obvodem, který modeluje i jejich frekvenční závislost. Výsledek je kompromisem mezi složitostí takového obvodu a jeho věrností vypočtenému originálu. Frekvenční závislost měrného odporu (prvku R/2n) je vlivem povrchového jevu ve sledovaných podmínkách pravděpodobně nejvýraznější. Je zřejmé, že v náhradním zapojení měrného odporu musí být použity i reaktanční prvky, takže výsledná impedance tohoto zapojení nebude čistě reálná. V určitém rozsahu lze frekvenční závislost měrného odporu vyjádřit jako odmocninu z frekvence. Z požadovaného průběhu měrného odporu je zřejmé, že impedanční funkce bude mít póly i nuly v nekonečnu a můžeme vycházet z kanonického zapojení RL členů. Koeficienty byly hledány nelineární regresí, s použitím funkce nlinfit v prostředí Matlab. Jako výsledný vektor hodnot byl použit vektor hodnot odporu vypočteného z modelu BT#1, hledanými parametry pak jsou hodnoty součástek. Musíme vzít na vědomí, že zapojením reaktančních prvků do obvodu imitujícího reálnou impedanci ztrácíme souvislost mezi úhlem přenosu skutečného vedení a obrazovým úhlem přenosu konstruovaného umělého vedení.
Na modulu impedance RL dvojpólu se vliv frekvenční závislosti měrné indukčnosti projeví mnohem více, než vliv závislosti měrného odporu. Nabízí se proto řešení vytvořit náhradní zapojení nikoli každého primárního parametru zvlášť, ale přímo sériového spojení prvků R/2n a L/2n. Vložením tohoto zapojení do segmentu vedení vznikne následující schéma, které je zobrazeno na Obr. 3.

Obr. 3 Modifikovaný segment vedení
A jeho impedanci je možno vyjádřit jako:
Nelineární regresí chceme zjistit hodnoty součástek tak, abychom došli k impedanci vypočtené z modelu BT#1, která má tvar:
Vlastní aproximace ukázala, že z náhradního schématu RL dvojpólu je možno vypustit induktor L3, který původně zastupoval měrnou indukčnost, neboť ta je dostatečně reprezentována induktory L1 a L2. Tato konstrukce umělého vedení je ve své podstatě velmi jednoduchá. Vychází z primárních parametrů skutečného vedení R, G, L, C a přípustných odchylek impedance či míry přenosu. Poměrná odchylka obrazové impedance od vlnové impedance skutečného vedení je po úpravách dána vztahem:
Poměrná odchylka ζ0 je číslo komplexní a bezprostředně závisí na měrném útlumu a posuvu nahrazovaného vedení a na počtu čtyřpólů n. Se vzrůstajícím počtem náhradních čtyřpólů na jednotku délky odchylka impedance rychle klesá. Z této rovnice lze odvodit vztah pro určení potřebného počtu segmentů:
kde ωmax je úhlová frekvence (fmax je nejvyšší frekvence přenášeného pásma).
Pomocí této návrhové metody by tedy bylo umělé vedení, pro přípojku ADSL o délce 4 km s horní mezní frekvencí 1 MHz, realizovatelné zapojením se 33 segmenty. Je-li ovšem každý segment upraven tak, aby respektoval frekvenční závislost primárních parametrů, potřebný počet segmentů pro zvolené pásmo podstatně roste.
Modelování jedním čtyřpólem
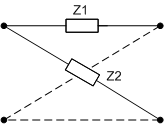
Zcela odlišný způsob konstrukce umělého vedení je založen na náhradě skutečného vedení délky l (km) dokonale souměrným křížovým článkem. Tato metoda je založena na aplikaci Barlettova teorému, podle kterého je možno každý příčně i podélně souměrný dvojbran nahradit zapojením dokonale souměrného křížového článku. Podélná impedance Z1 odpovídá impedanci nakrátko vedení poloviční délky, vzhledem k vedení modelovanému, a podobně diagonální impedance Z2 odpovídá impedanci naprázdno vedení poloviční délky. S úspěchem bude touto metodou zkonstruováno umělé vedení tehdy, jestliže se podaří nalézt zapojení, jejichž impedance odpovídá impedanci naprázdno a nakrátko poloviční délky modelovaného vedení v zadaném frekvenčním rozsahu. Zapojení dokonale souměrného křížového článku je na Obr. 4.
Obr. 3 Základní zapojení křížového článku
Jeho impedance naprázdno a nakrátko jsou dány rovnicemi:
Obrazová impedance je dána vztahem:
a obrazovou míru přenosu lze vyjádřit jako:
Křížový článek je ekvivalentem homogenního vedení délky l (km). Poté lze tedy řešit rovnice postupným rozvojem v řetězový zlomek. Podle řetězových zlomků poté sestavíme řetězové dvojpóly, které realizují jejich impedance.
Oba řetězové zlomky i řetězové dvojpóly mají nekonečný počet členů. V praxi se ovšem musíme spokojit s konečným počtem členů a tím vzniknou odchylky mezi zadanou a aproximující funkcí. Připomínám, že křížový článek napodobuje vedení délky 2l (km). Metoda je efektivní pouze za předpokladu, že rozdíl obou impedancí je významně větší, než chyba aproximace. Pro tento způsob konstrukce umělého vedení podstatné, aby se obě impedance významně lišily. Rozdíl obou impedancí tedy je:
Vztáhneme-li tento rozdíl k hodnotě charakteristické impedance , bude tato poměrná odchylka činit:
Zkracováním délky vedení rozšiřujeme frekvenční pásmo, ve kterém je rozdíl impedancí nakrátko a naprázdno takový, že umožňuje konstrukci umělého vedení pomocí této metody. Nabízí se tedy možnost zkonstruovat umělé vedení pro kratší úseky vedení, a následně jejich kaskádním spojením realizovat vlastnosti vedení požadované délky. Zde ovšem narážíme na další omezení této metody, kterým je požadavek na snadnou realizovatelnost impedančních funkcí. Prvním omezujícím faktorem je útlum vedení, který závisí na primárních parametrech a délce vedení. Čím vyšší je jeho hodnota, tím menší je rozdíl impedance naprázdno a nakrátko a tím vyšší požadavky na přesnost aproximace. Druhým omezujícím faktorem je realizovatelnost impedanční funkce, tj. omezení na takové frekvenční pásmo, při kterém nenastane rovnost mezi délkou vedení a čtvrtinou vlnové délky. Z principu této metody ovšem nevyplývá podmínka, aby délka vedení byla menší než čtvrtina vlnové délky.
Závěr
Využití známých metod návrhu umělých vedení ve snaze upravit je tak, aby výsledný obvod simuloval parametry skutečného vedení v daném frekvenčním rozsahu, tj. pro digitální účastnické přípojky, přineslo následující zjištění:
- metoda s použitím n segmentů vedení je vhodná pro omezené frekvenční pásmo, s tím, že obvodové modelování primárních parametrů skutečného vedení výrazně zvyšuje potřebný počet segmentů vedení,
- metoda s použitím křížového článku je vhodná pro úzké frekvenční pásmo a vedení s nízkým útlumem.
Omezení jednotlivých metod nám bohužel neumožňují úspěšné navržení umělého vedení, jež by splňovalo požadavky na jednoduchost zapojení obvodu (tj. pokud možno minimální počet stavebních prvků obvodu) pro dané provozní podmínky (délku a frekvenční pásmo).
Bylo tedy nutné přistoupit k návrhu umělého vedení jiným způsobem, tzv. experimentální metodou, která je popsána v navazujícím článku „Modul umělého vedení pro digitální účastnické přípojky“, kde je také popsán finální návrh včetně realizace a ověření vlastností umělého vedení.
Příspěvek vznikl za podpory výzkumného záměru MSM6840770014 - Výzkum perspektivních informačních a komunikačních technologií.
Literatura
[1] Skilling, Hugh Hildreth: Electric Transmission lines: Distributed Constants, Theory and Applications, New York: McGraw-Hill Book Company, 1951.
[2] Johson, Walter C.: Transmission Lines and Networks, New York: McGraw-Hill Book Company, 1950.
[3] Matik, Richard E.: Transmission Lines for Digital and Communication Networks: An Introduction to Transmission Lines, High-frequency and High-Speed Pulse Characteristics and Applications, New York: McGraw-Hill Book Company, 1969.
[4] Kvasil, Josef: Elektrické lineární obvody, Praha: Nadas, 1967.