|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
Témata
Doporučujeme
Kontakt
|

Vydáno dne 16. 12. 2005 (12146 přečtení) |
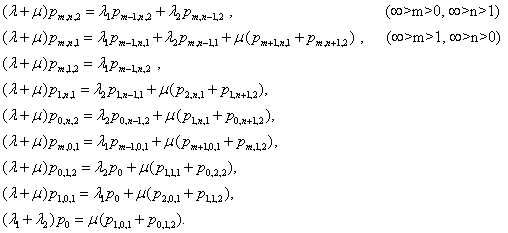 | (1) |
Pro vyřešení soustavy rovnic (1) lze použít generující funkce. Definujme
 | (2) |
H(y,z) je generující funkce pro dvě prioritní třídy bez ohledu na to, který požadavek je v obsluze. Všimněme si, že H(1,1)=1, H1(1,1)=λ1/µ , H2(1,1)=λ2/µ a p0=1-λ/µ. Označme střední počet požadavků v systému jako E[X1] a E[X2]. Potom platí
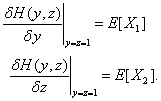 | (3) |
S využitím Littlova vzorce a rovnic (3) můžeme určit střední dobu zdržení požadavků obou toků – E[X1], E[X2] tak, že platí
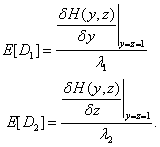 | (4) |
Pro získání závislosti střední doby zdržení na intenzitě příchodů - λ1 a λ2, je nutné plně určit generující funkci H(y,z). Úpravou rovnic (1) lze nalézt vztahy
 | (5) |
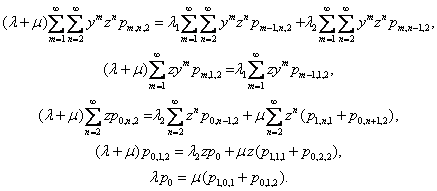 | (6) |
Nyní rozdělme funkci H(y,z) (2) na dvě části H1(y,z), H2(y,z). Součtem rovnic (5) s přihlédnutím k rovnicím (2) po algebraické úpravě dostáváme
| | (7) |
Obdobně pro H2(y,z) dostaneme ze soustavy rovnic (6)
| | (8) |
Úplné určení funkce H(y,z) vyžaduje určení P11(z) a P02(z). Funkce P11(z) a P02(z) určíme z rovnic (1) a (2). Platí
| | (9) |
| | (10) |
Z rovnic (2), (7), (8), (9) a (10) odvodíme vztah pro generující funkci H(y,z) ve tvaru
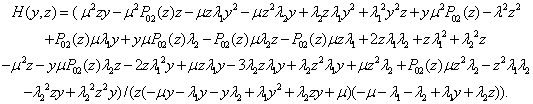 | (11) |
Užitím (4) dostaneme pro E[X1] a E[X2]
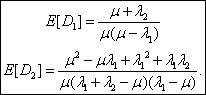 | (12) |
Předpokládejme, že do síťového uzlu realizovaného směrovačem přichází dva toky paketů s nabídkami A1=A2=0,1 erl (A1=λ1/µ A2=λ2/µ. Intenzita obsluhy je pro oba toky stejná µ=1/tos =1/120. Dále předpokládejme, že tok s nabídkou A1 je prioritní (tj. má vyšší prioritu než tok s nabídkou A2 ), router má nekonečnou kapacitu paměti a že rozdělení doby mezi příchody požadavků a doby obsluhy jsou exponenciální. Zajímá nás, jaké je průměrné zpoždění paketů ve směrovači.
Za výše uvedených předpokladů je možné popsat směrovač pomocí obsluhového systému s čekáním. K výpočtu zpoždění (střední hodnoty doby zdržení požavku v obsluhovém systému) je pak možné použít vztahy (12). Výsledky jsou uvedeny v následující tabulce.

Kromě výsledku příkladu jsou uvedeny v tabulce č.1 výsledky pro další velikosti nabídek A1, A2 a pro různé velikosti střední doby obsluhy tos. Zajímala-li by nás závislost středních dob zdržení požadavků na nabídce, obdrželi bychom následující grafy.
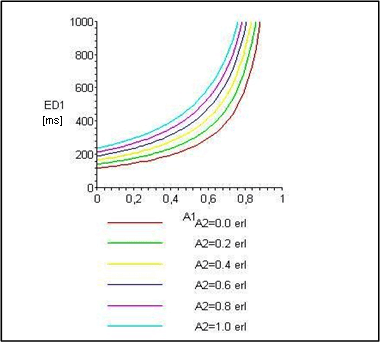
Obr. 1 Závislost střední doby zdržení E[D1] na nabídce A1
Na obrázku č. 1 je znázorněna závislost střední doby zdržení prioritního toku E[D1] na nabídce A1. Zobrazeny jsou průběhy pro nabídky toku s nižší prioritou A2=0 erl až A2 =1 erl. Všimněme si, že střední doba zdržení prioritního toku vždy od určité hodnoty nabídky A1 začíná strmě růst do nekonečna a že tato hodnota se liší pro různé velikosti nabídky A2. Tomu odpovídá fakt, že pro obsluhový systém s čekáním by neměla celková nabídka A=A1+A2 být větší než počet obsluhových linek (v našem případě jedna).
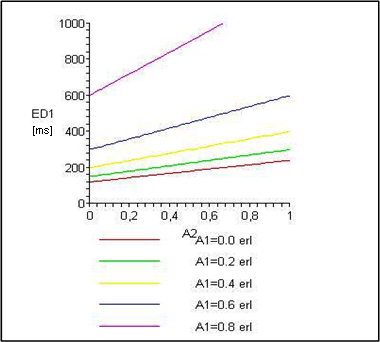
Obr. 2 Závislost střední doby zdržení E[D1] na nabídce A2
Na obrázku č. 2 je znázorněna závislost střední doby zdržení prioritního toku E[D1] na nabídce neprioritního toku A2. Jedná se o lineární závislost naznačující, že velikost nabídky A2 ovlivňuje střední dobu zdržení prioritního toku E[D1] . To může být na první pohled matoucí. Uvědomíme-li si však, že veškeré použité veličiny mají nahodný charakter, zjistíme, že s rostoucí nabídkou A2 roste pravděpodobnost výskytu jevu příchodu prioritního požadavku do systému v okamžiku obsluhy neprioritního požadavku. S růstem této pravděpodobnosti dochází k nárustu střední hodnoty doby zdržení E[D1].
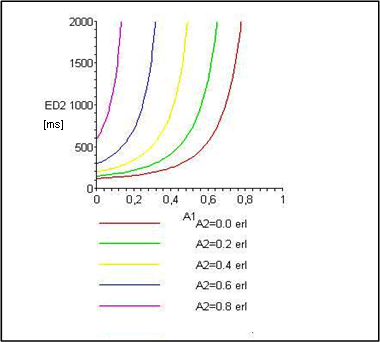
Obr. 3 Závislost střední doby zdržení E[D2] na nabídce A1
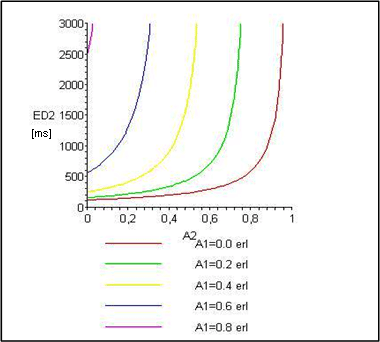
Obr. 4 Závislost střední doby zdržení E[D2] na nabídce A2
Na obrazcích č. 3 a č. 4 jsou znázorněny závislosti střední doby zdržení požadavků neprioritního toku E[D2] na nabídkách A1 a A2.
Příspěvek se zaměřuje na odvození střední doby zdržení toků o intenzitách λ1 a λ2, z nichž tok první je prioritní (tzv. slabá priorita), v obsluhovém systému představujícím síťový uzel (směrovač). Byly odvozeny vztahy (12). Díky omezenému rozsahu článku bylo použito speciálního zápisu vztahů a některé vypočetní operace byly pouze naznačeny.
Do budoucna se plánuje porovnání vztahů
Tento příspěvek vznikl za podpory grantu č. 1ET300750402 Grantové Agentury Akademie Věd České Republiky.
[1] Morse, P.M. Queues, Inventories and Maintenance. New York: Wiley. 1958
[2] Gross, Donald. Harris, M. Carl. Fundamentals of Queuing Theory (Third
Edition). John Wiley & Sons. New York. 1998
[3] Konopka, Lukáš. Delay of
Packets in Queuing System with Priorities. Sborník RTT 2005. VŠB Ostrava.
2005
Tento web site byl vytvořen prostřednictvím phpRS - redakčního systému napsaného v PHP jazyce.
Na této stránce použité názvy programových produktů, firem apod. mohou být ochrannými známkami
nebo registrovanými ochrannými známkami příslušných vlastníků.