|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
Témata
Doporučujeme
Kontakt
|

Vydáno dne 21. 07. 2010 (14929 přečtení) |
 | (1) |
 | (2) |
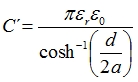 | (3) |
|
| (4) |
Tab. 1: Parametry kabelu CYKY 3x2.5
|
Označení |
Význam |
Rozměr (jednotka) |
|
a |
Poloměr vodiče |
0,892 mm |
|
d |
Vzdálenost mezi středy vodičů |
3,584 mm |
|
σ |
Konduktivita mědi |
58•106 S•m-1 |
|
μ0 |
Permeabilita vzduchu |
4• π• 10-7 H•m-1 |
|
μr |
Relativní magnetická permeabilita mědi |
0,99999 |
|
ε0 |
Permitivita vakua |
8,854•10-12 F•m-1 |
|
εr |
Relativní permitivita izolace |
4 |
 | (5) |
 | (6) |
 | (7) |
Dále je nutné provést výpočet koeficientů přenosu podle rovnic:
|
| (8) |
|
| (9) |
Šíření signálu od vysílače k přijímači může probíhat v odlišných cestách, možné cesty jsou znázorněny v Tab. 2.
Tab. 2: Šíření signálu od vysílače k přijímači pro ukázkovou síť
|
Číslo cesty |
Směr cesty |
Váha cesty gi |
Délka cesty di |
|
1 |
A-B-C |
t1B |
l1+l2 |
|
2 |
A-B-D-B-C |
t1B•r3D•t3D |
l1+2l3+l2 |
|
... |
|||
|
N |
A-B (-D-B)N-1-C |
t1B•r3D• (r3B•r3D)(N-2)•t3D |
l1+2(N-1)l3+l2 |
Každá cesta i má svou váhu gi reprezentující odrazy a faktory přenosu podél cesty. Zpoždění cesty τi lze vypočíst z délky cesty, rychlosti světla ve vakuu c0 a relativní permitivity izolace εr podle rovnice:
 | (10) |
Signál od vysílače k příjemci se může šířit nekonečným počtem cest v závislosti na topologii sítě. Zvětšováním počtu cest N můžeme zvyšovat přesnost modelu. Jelikož útlum vedení A(f,d) roste s délkou a frekvencí, tak s rostoucí délkou cesty je útlum větší a proto je menší váha cesty a tím méně přispívá váha této cesty do celkového signálu na straně příjemce. Z toho důvodu není nutné volit příliš mnoho cest. Pro výpočet bylo zvoleno počet cest N=6.
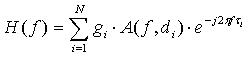 | (11) |
Rovnice (11) reprezentuje přenosovou funkci silnoproudého vedení pro prostředí s vícecestným šířením. Na základě těchto výpočtu byla zjištěna přenosová funkce ukázkové sítě, parametry modelu jsou v Tab. 3 a frekvenční odezva je zobrazena Obr. 2.
Tab. 3: Šíření signálu od vysílače k přijímači pro ukázkovou síť
|
Číslo cesty |
1 |
2 |
3 |
4 |
5 |
6 |
|
di |
200 |
238 |
276 |
314 |
352 |
390 |
|
gi |
0,6664 |
0,2498 |
-0,0408 |
0,0067 |
-0,0011 |
0,0002 |

Obr. 2: Simulace ukázkové sítě pro 6 cest
Přenosová funkce kaskádně zapojených dvojbranuDalší možností modelování silnoproudých vedení je pomocí kaskádních parametrů, které popisují závislost vstupních a výstupních napětí a proudů pomocí dvojbranu. Budeme-li uvažovat ukázkový model na Obr. 1 s jednou odbočkou a tu nahradíme odpovídající impedancí Zeq. Dále budeme uvažovat, že vysílač a přijímač jsou impedančně nepřizpůsobené kabelu, na který jsou připojeny, tudíž zde bude docházet k odrazům a spotřebič na odbočce má impedanci Zbr. Impedanci odbočky vypočteme podle rovnice [6]:
|
| (12) |
kde Zbr a γbr jsou charakteristická impedance a měrný činitel přenosu pro odbočku. Tab. 4 zobrazuje parametry ukázkové distribuční sítě na Obr. 1 a vypočtené hodnoty pro kaskádní zapojení.
Tab. 4:Parametry ukázkové distribuční sítě
|
ZS |
120 Ω |
|
ZL |
600 Ω |
|
Zbr |
300 Ω |
|
Z |
180 Ω |
|
Zeq |
97,67-0,669i Ω |

Obr. 3: a)Vedení s jednou odbočkou. b) Zjednodušené vedení s jednou odbočkou
Na Obr. 3 b) je vedení s jednou odbočkou zobrazeno jako vícenásobné zapojení elementárních dvojbranů, které jsou popsány maticemi A1 až A4:
|
| (13) |
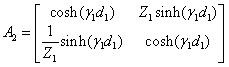 | (14) |
 | (15) |
 | (16) |
kde Z1,γ1, Z2 a γ2 jsou charakteristická impedance a měrný činitel přenosu pro druhý a čtvrtý dvojbran.
Výslednou kaskádní matici modelovaného vedení s jednou odbočkou získáme jako součin dílčích kaskádních matic:
|
| (17) |
kde n je počet dílčích částí popsaných kaskádní maticí. Známe-li parametry ABCD výsledné kaskádní matice, můžeme určit přenosovou funkci pomocí rovnice:
 | (18) |
Na základě tohoto výpočetního aparátu byla zjištěna přenosová funkce ukázkového modelu a frekvenční odezva je zobrazena na Obr. 4. Odrazy v nepřizpůsobené odbočce způsobí periodické zvlnění ve frekvenční odezvě.

Obr. 4: Simulace ukázkové sítě pro impedančně nepřizpůsobený vysílač, přijímač a odbočku
Z přenosové funkce prostředí s vícecestným šířením anebo z přenosové funkce dvojbranu byly vypočteny koeficienty FIR filtru a těmito filtry bylo modelováno silnoproudé vedení společně se zdroji rušení. Detailní popis zdrojů rušení a jejich modelů můžeme najít v [7]. Na Obr. 5 je zobrazen výsledný model kanálu modelovaný pomocí přenosové funkce společně se zdroji rušení. Tento model kanálu umožní co nejpřesněji simulovat datovou komunikaci po silnoproudých vedeních.

Obr. 5: Výsledný model kanálu
Tento příspěvek vznikl za podpory výzkumného záměru Ministerstva školství, č. MSM 0021630513 a grantu FEKT-S-10-16.
[1] The MathWorks [online]. 1999 [cit. 2010-05-05]. Online: http://www.mathworks.com
[2] CATALIOTTI, A.; DAIDONE, A.; TINE, G. Power line communications in Medium Voltage system: Characterization of MV cables. IEEE Transactions on Power Delivery, vol. 23, n. 4, 2008.
[3] PAPALEONIDOPOULOS, I.; KARAGIANNOPOULOS, C.; THEODOROU, N.; ANAGNOSTOPOULOS, C.; ANAGNOSTOPOULOS, I. Modelling of indoor low voltage power-line cables in the high frequency range. International Symposium on Power Line Communications and Its Applications (ISPLC).
[4] ZIMMERMANN, M.; DOSTERT, K. A Multi-Path Signal Propagation Model for the Power Line Channel in the High Frequency Range. Proceedings of the 3rd International Symposium on Power-Line Communications, Lancaster, UK, 1999, pp. 45 – 51.
[5] ZIMMERMANN, M; DOSTERT, K. A Multipath Model for the Powerline Channel. IEEE Transactions on Communications. 2002, VOL. 50, NO. 4.
[6] ESMAILIAN, T; KSCHISCHANG, F; GULAK, G. In-building power lines as high-speed communication channels: channel characterization and a test channel ensemble. International Journal of Communication Systems. 2003.
[7] BABIC, M.; HAGENAU, M.; DOSTERT, K.; BAUSCH, J. Theoretical postulation of PLC channel model. Open PLC European Research Alliance (OPERA). 2005
Tento web site byl vytvořen prostřednictvím phpRS - redakčního systému napsaného v PHP jazyce.
Na této stránce použité názvy programových produktů, firem apod. mohou být ochrannými známkami
nebo registrovanými ochrannými známkami příslušných vlastníků.