|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
 |
ISSN 1214-9675 Server vznikl za podpory Grantové agentury ČR. 21. ročník |
|
Témata
Doporučujeme
Kontakt
|
Vydáno dne 17. 09. 2012 (9532 přečtení) |
 | (1), (2), (3) |
Manhattanská vzdálenost (Manhattan distance, City Block distance, Boxcar distance, Rectilinear distance, Absolute Value distance) reprezentuje vzdálenost mezi dvěma body, které si lze představit jako křižovatky v silniční síti městské zástavby. Jde o vzdálenost vyjádřenou jako sumu horizontálních a vertikálních cest z bodu A do bodu B (jako by se šlo po ulicích kolem budov a není možné jít přímo, diagonálně). Tato vzdálenost je speciálním případem Minkowského vzdálenosti s parametrem λ = 1. Je vždy větší nebo rovna nule (pro identické body) a vyšší pro body vykazující menší podobnost. Využívá se hojně v integrovaných obvodech, kde jsou vodiče vedeny paralelně k ose X nebo Y, nefunguje příliš dobře pro zpracování obrazových dat a klasifikace dokumentů. Vzdálenost se vypočítá podle vzorce:
 | (4) |
Čebyševova vzdálenost (Maximum Value distance) prozkoumává absolutní velikost odlišností mezi souřadnicemi dvou objektů. Tato vzdálenost může být použita pro ordinální i kvantitativní proměnné. Jde o speciální případ Minkowského vzdálenosti s parametrem λ = ∞. Tato vzdálenost je výhodná pro objekty, jejichž odlišnost se posuzuje spíše podle individuálních parametrů než podle všech parametrů objektu jako celku. Vzdálenost se vypočítá podle vzorce:
 | (5) |
Minkowského vzdálenost je obecnou metrikou pro měření vzdálenosti. Souvztažnost s jinými typy vzdáleností (hodnota parametru lambda) byla zmíněna v jednotlivých odstavcích výše. Vzdálenost se hodí pro měření jak ordinálních, tak kvantitativních proměnných a vypočítá se podle vzorce:
 | (6) |
Canberrova vzdálenost jedná se o metriku, která je definována jako absolutní hodnota vzdálenosti mezi proměnnými dvou objektů podělená sumou absolutních hodnot těchto proměnných. Každý výsledek tohoto podílu odlišnosti zlomku má hodnotu mezi 0 a +1. Tato vzdálenost sama o sobě ovšem hodnotu mezi 0 a +1 mít nemusí. Je používána, pokud jsou měřené body v blízkosti jejich vzniku a je velmi citlivá pro hodnoty blížící se nule. Tato vzdálenost je velmi citlivá na malé změny pokud se obě souřadnice nachází blízko nule. Její výpočet se provede podle vzorce:
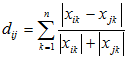 | (7) |
Bray-Curtisova vzdálenost (Sorensenova vzdálenost, Czekanowski’s coefficient) je normalizovanou metodou používanou často v botanice, ekologii a environmentálních vědách. Nahlíží na problém podobně jako Manhattanská vzdálenost (mřížka představující silniční síť v městské zástavbě). Vzdálenost má tu dobrou vlastnost, že pokud jsou všechny souřadnice pozitivní, jejich hodnoty jsou mezi nulou a jedničkou. Normalizace je provedena použitím absolutní odlišnosti dělené sumou součtu hodnot proměnných. Výpočet této vzdálenosti je dán vzorcem:
 | (8) |
V rámci zkoumání citlivosti metod pro měření vzdálenosti mezi dvěma body bylo provedeno dvanáct měření. Během prvních tří měření byla zkoumána citlivost metod při měření vzdálenosti hodnot blížícím se nule. Souřadnice bodu A byly nastaveny a hodnoty (0,001;0,001) a bodu B na hodnoty (0,01;0,01). Změřené vzdálenosti pro tyto body jsou zaneseny v tabulce 1 jako „Měření 1“. Při druhém měření byla provedena změna souřadnic bodu A na (0,002;0,001) a opět byla změřena vzdálenost bodu A a bodu B. U třetího měření byl bod A nastaven na souřadnice (-0,001;0,001). Ve všech tabulkách se vyskytují měření těmito metodami: Euklidovská vzdálenost, Manhattanská vzdálenost, Čebyševova vzdálenost, Minkowského vzdálenost s parametrem λ = 3, Canberrova vzdálenost a Bray-Curtisova vzdálenost. V každé tabulce je také vidět absolutní rozdíl a relativní odchylka mezi první a druhým měřením (v rámci tabulky) a první a třetím měřením (v rámci tabulky), z čehož je možné usoudit, která metoda bude pro požadované měření vzdálenosti výhodnější.
Tabulka 1 : Měření vzdálenosti dvou bodů blížících se nule.
|
|
Měření 1 |
Měření 2 |
Absolutní rozdíl měření 1 a měření 2 |
Relativní odchylka měření 1 a měření 2 |
Měření 3 |
Absolutní rozdíl měření 1 a měření 3 |
Relativní odchylka měření 1 a měření 3 |
|
A1=0,001 A2=0,001 |
A1=0,002 A2=0,001 |
A1=-0,001 A2=0,001 |
|||||
|
B1=0,01 B2=0,01 |
B1=0,01 B2=0,01 |
B1=0,01 B2=0,01 |
|||||
|
Euclidean |
0,0127 |
0,0120 |
0,0007 |
2,83% |
0,0142 |
0,0015 |
5,58% |
|
Manhattan |
0,0180 |
0,0170 |
0,0010 |
2,86% |
0,0200 |
0,0020 |
5,26% |
|
Čebyšev |
0,0090 |
0,0090 |
0 |
0,00% |
0,0110 |
0,0020 |
10,00% |
|
Minkowski |
0,0113 |
0,0107 |
0,0006 |
2,73% |
0,0127 |
0,0014 |
5,83% |
|
Canberra |
1,6363 |
1,4848 |
0,1515 |
4,85% |
1,8181 |
0,1818 |
5,26% |
|
Bray-Curtis |
0,8181 |
0,7391 |
0,0790 |
5,07% |
1,0000 |
0,1819 |
10,00% |
V dalších třech měřeních byla měřena citlivost metod pro měření vzdálenosti mezi dvěma body, kdy body dosahují relativně vysokých hodnot (vzdálených od nuly). V měření 4 byly souřadnice bodu A nastaveny na hodnoty (1000;1000) a souřadnice bodu B na hodnoty (100; 100). Bylo provedeno měření těchto zadaných bodů, při dalším měření byl změněn bod A na souřadnice (1002;1000) a vypočítána jeho vzdálenost k původnímu bodu B. U šestého měření byl bod A změněn na souřadnice (-1000;1000) a vypočítána vzdálenost opět k původnímu bodu B. V tabulce 2 jsou uvedeny vypočítané hodnoty vzdálenosti pro tyto další tři měření.
Tabulka 2 : Měření vzdálenosti dvou bodů vzdálenějších od nuly.
|
|
Měření 4 |
Měření 5 |
Absolutní rozdíl měření 4 a měření 5 |
Relativní odchylka měření 4 a měření 5 |
Měření 6 |
Absolutní rozdíl měření 4 a měření 6 |
Relativní odchylka měření 4 a měření 6 |
|
A1=1000 A2=1000 |
A1=1002 A2=1000 |
A1=-1000 A2=1000 |
|||||
|
B1=100 |
B1=100 |
B1=100 |
|||||
|
Euclidean |
1272,7922 |
1274,2072 |
1,4150 |
0,0556% |
1421,2670 |
148,4748 |
5,51% |
|
Manhattan |
1800,0000 |
1802,0000 |
2,0000 |
0,0555% |
2000,0000 |
200,0000 |
5,26% |
|
Čebyšev |
900,0000 |
902,0000 |
2,0000 |
0,1110% |
1100,0000 |
200,0000 |
10,00% |
|
Minkowski |
1133,9289 |
1135,1902 |
1,2613 |
0,0556% |
1272,3963 |
138,4674 |
5,75% |
|
Canberra |
1,6363 |
1,6367 |
0,0004 |
0,0122% |
1,8181 |
0,1818 |
5,26% |
|
Bray-Curtis |
0,8182 |
0,8183 |
0,0001 |
0,0061% |
10,0000 |
9,1818 |
84,87% |
V předposledních třech měřeních byl použit jeden bod se souřadnicemi od nuly vzdálenějšími A = (1000;1000) a jeden bod velmi blízko nule B = (0,001;0,001). Výsledky měření vzdálenosti těchto dvou bodů jsou uvedeny v tabulce. Při sedmémměření byly změřeny vzdálenosti originálních bodů A a B. Při osmém měření byl bod A lehce posunut na souřadnice A = (1002;1000) a opět změřena vzdálenost k bodu B. V devátém měření byly souřadnice bodu A nastaveny na souřadnice (-1000;1000) a změřena vzdálenost k původnímu bodu B.
Tabulka 3 : Měření vzdálenosti bodu blížícího se nule a bodu vzdálenějšího od nuly.
|
|
Měření 7 |
Měření 8 |
Absolutní rozdíl měření 7 a měření 8 |
Relativní odchylka měření 7 a měření 8 |
Měření 9 |
Absolutní rozdíl měření 7 a měření 9 |
Relativní odchylka měření 7 a měření 9 |
|
A1=1000 A2=1000 |
A1=1002 A2=1000 |
A1=-1000 A2=1000 |
|||||
|
B1=0,001 B2=0,001 |
B1=0,001 B2=0,001 |
B1=0,001 B2=0,001 |
|||||
|
Euclidean |
1414,2121 |
1415,6271 |
1,4150 |
0,0500% |
1414,2136 |
0,0015 |
0,0001% |
|
Manhattan |
1999,9980 |
2001,9980 |
2,0000 |
0,0500% |
2000,0000 |
0,0020 |
0,0001% |
|
Čebyšev |
999,9990 |
1001,9990 |
2,0000 |
0,0999% |
1000,0010 |
0,0020 |
0,0001% |
|
Minkowski |
1259,9198 |
1261,1891 |
1,2693 |
0,0503% |
1259,9211 |
0,0013 |
0,0001% |
|
Canberra |
1,9999 |
1,9999 |
0 |
0,0000% |
1,9999 |
0 |
0,0000% |
|
Bray-Curtis |
0,9999 |
0,9999 |
0 |
0,0000% |
1.000e+6 |
9,999e+5 |
- |
V posledních třech měřeních je demonstrováno rozložení bodu, kdy vždy jeden z bodů má jednu souřadnici blížící se nule a jednu rapidně vzdálenější. Pří těchto měřeních se ukázalo, že téměř všechny použité metody dosahují stejných neb o velice podobných výsledků. Pro desáté měření byl bod A nastaven na souřadnice (0,01;1000) a bod B na souřadnice (0,001;1000). V jedenáctém měření byl bod A posunut na souřadnice (0,01;1002) a bod B zůstal zachován. V posledním, dvanáctém měření byl bod A posunut na souřadnice (-0,01;1000) a bod B zůstal opět zachován. Výsledky jsou zaneseny v tabulce 4.
Tabulka 4 : Měření vzdálenosti bodů, kde se jedna souřadnice blíží nule a druhá je výrazně vyšší.
|
|
Měření 10 |
Měření 11 |
Absolutní rozdíl měření 10 a měření 11 |
Relativní odchylka měření 10 a měření 11 |
Měření 12 |
Absolutní rozdíl měření 10 a měření 12 |
Relativní odchylka měření 10 a měření 12 |
|
A1=0,01 A2=1000 |
A1=0,01 A2=1002 |
A1=-0,01 A2=1000 |
|||||
|
B1=0,001 B2=1000 |
B1=0,001 B2=1000 |
B1=0,001 B2=10000 |
|||||
|
Euclidean |
0,0090 |
2,0000 |
1,9910 |
99,1040% |
0,0110 |
0,0020 |
10,0000% |
|
Manhattan |
0,0090 |
2,0090 |
2,0000 |
99,1080% |
0,0110 |
0,0020 |
10,0000% |
|
Čebyšev |
0,0090 |
2,0000 |
1,9910 |
99,1040% |
0,0110 |
0,0020 |
10,0000% |
|
Minkowski |
0,0090 |
2,0000 |
1,9910 |
99,1040% |
0,0110 |
0,0020 |
10,0000% |
|
Canberra |
0,8181 |
0,8192 |
0,0011 |
0,0672% |
1,0000 |
0,1819 |
10,0050% |
|
Bray-Curtis |
4,499e-6 |
0,0010 |
9,955e-4 |
99,1042% |
5,500e-6 |
1,001e-6 |
10,0110% |
K vyhodnocování citlivosti metod měřících vzdálenost mezi objekty můžeme přistupovat ze dvou hledisek. První hledisko dává důraz na odlišení objektů za každou cenu, i když mají velmi podobné hodnoty příznaků (souřadnice). Mezi velmi podobnými hodnotami některé z metod již rozdíl nerozlišují, tedy některé metody nemají dostatečnou rozlišovací schopnost, aby byl rozdíl vidět na první pohled (zde může jít například o číslicové vyjádření na určitý počet desetinných míst) a byť jde o rozdílné souřadnice dvou objektů, jsou tyto objekty reprezentovány jako jeden identický objekt. V případě, že má být rozlišovací schopnost maximální, je vhodné zvolit takovou metodu, která má mezi podobnými hodnotami příznaků dvou objektů takové výsledky, jejichž rozdíl je větší než u jiných metod s rozlišovací schopností na velký počet desetinných míst.
Druhým přístupem je nahlížení na problematiku metod měřících vzdálenost mezi objekty z hlediska šumu. Tento přístup je přesným opakem předchozího. V podstatě jde o to, aby byla zvolena taková měřící metoda, která rozlišuje objekty, až od určité vzdálenosti tzn., že se dokáže vyrovnat se šumem, který mohl mírně změnit hodnoty příznaků (souřadnice) objektu, ale jedná se pořád o tentýž objekt, pouze posunutý o určitou minimální vzdálenost. Na základě těchto dvou přístupů, lze jednoduše vybrat, jakou měřící metodu budeme v projektu používat. V případě, že má být rozlišovací schopnost metod odolná vůči informačnímu šumu a hodnoty příznaků jednoho objektu mohou být posunuty, je třeba zvolit metodu s odpovídající rozlišovací schopností, která rozlišuje objekty až od určité vzdálenosti.
Dále byl také do všech tabulek přidán výsledek výpočtu, který znázorňuje relativní odchylku vždy mezi první a druhým měřením v rámci tabulky a mezi prvním a třetím měřením v rámci tabulky. Tato relativní odchylka ovšem nemusí být vždy jednoznačně vypovídající o výsledku, jelikož z ní není patrná citlivost metod – tedy, na kolik desetinných míst je výsledek vyjádřen, a i když je relativní odchylka vysoká (nyní bereme v potaz maximální rozlišovací schopnost metody v tabulce 1, metoda Čebyšev), nemusí být metoda nejlepší, jelikož nebere v potaz desetinná místa. Na základě tohoto zjištění doporučujeme posuzovat výsledek ne jen podle relativní odchylky, ale i podle absolutního rozdílu daných měření, který znázorňuje požadovanou citlivost na měřená data.
Obecně lze říci, že využití Euklidovské vzdálenosti nebo Čtvercové Euklidovské vzdálenosti je použitelné ve všech případech, i když se nejedná o ideální přístup. Rozlišovací schopnost této měřící metody čítá desetinná místa a je schopna měřit nejen vzdálenosti blízké či vzdálené od nuly, ale i jejich kombinace. Tuto metodu si stanovíme jako referenční a budeme její výsledky porovnávat s výsledky ostatních testovaných metod.
Pokud měříme hodnoty blížící se nule (viz tabulka 1), je jednoznačně nejlepší a nejpřesnější volbou měřit vzdálenost pomocí Canberrovy vzdálenosti. Pomocí této vzdálenosti lze změřit i velmi malé rozdíly mezi objekty. S podobnou přesnosti u takto malých hodnot pracuje i Bray-Curtisova vzdálenost. Pokud se budeme dívat na problém měření hodnot blížících se nule z druhé strany, tedy metody musí vykazovat jistou odolnost vůči šumu, je vhodné použít např. metodu Čebyševovy vzdálenosti, která malé rozdíly při měření vzdálenosti nereflektuje.
V případě měření hodnot vzdálenějších od nuly – viz tabulka 2, vychází měření v případě citlivosti příznivě pro Minkowského metriku a Euklidovskou vzdálenost, která mají velmi dobrou rozlišovací schopnost právě pro hodnoty vzdálenější od nuly. Naopak, při takto zadaných hodnotách selhává právě Canberrova a Bray-Curtisova vzdálenost, které pro výsledné hodnoty nevykazují téměř žádnou vzdálenost. Stejný případ je měření vzdálenosti bodu vzdálenějšího od nuly a bodu blízkého nule - viz tabulka 3, kdy se osvědčilo měření vzdálenosti pomocí Euklidovské vzdálenosti a Minkowského metriky a selhání Canberrovy a Bray-Curtisovy vzdálenosti. V posledních třech měřeních je demonstrováno rozložení bodu, kdy vždy jeden z bodů má jednu souřadnici blížící se nule a jednu rapidně vzdálenější – viz tabulka 4. Z naměřených výsledku je vidět, že metody dosahují téměř stejných nebo podobných výsledků, až na metody měření Canberrovy a Bray-Curtisovy vzdálenosti, které jsou vhodnější pro měření bodů blízkých nule. Na základě těchto výsledků lze pro měření doporučit obecnou a známou Euklidovskou vzdálenost.
Tento článek zkoumá existující metody pro měření vzdálenosti mezi objekty využívané např. v algoritmech pro shlukovou analýzu dat. Článek se konkrétně zabývá zkoumáním citlivosti metod na analyzovaná data a jeho výstupem je srovnání těchto metod a doporučení, v jakém případě by měla být která metoda použita. Toto srovnání pomůže dalším výzkumníkům v dané oblasti při rychlém rozhodování, kterou metodu pro měření vzdálenosti v dané situaci použít. Pro měření vzdáleností bodů se souřadnicemi blížícími se nule je vhodné využít Canberrovu nebo Bray-Curtisovu vzdálenost. Pro hodnoty vzdálenější od nuly a hodnoty nejrůznějšího charakteru je vhodné použít Minkowského metriku s parametrem ?=3 a Euklidovskou vzdálenost.
Vznik článku byl podpořen výzkumným projektem Ministerstva průmyslu a obchodu ČR, č. FR-TI4/151 a interním grantem Fakulty elektrotechniky a komunikačních technologií Vysokého učení technického, evidenční č. FEKT-S-11-17.
[1] Deza, M. M.; Deza E.; Encyclopedia of Distances. Springer-Verlang Berlin Heidelberg, 2009, s. 583, [online] Dostupné z www:
http://www.uco.es/users/ma1fegan/Comunes/asignaturas/vision/ Encyclopedia-of-distances-2009.pdf
[2] Kardi, T.; Similarity Measurement. 2006. [online] Dostupné z www:
http://people.revoledu.com/kardi/tutorial/Similarity/
[3] Pandit, S., Gupta, S.; A comparative study on distance measuring approaches for clustering, International Journal of Research in Computer Science, vol. 2, issue 1, s. 29-31, 2011, ISSN 2246-8265
[4] Vimal, A.; Valluri, S. R.; Karlapalem, K.; An Experiment with Distance Measures for Clustering, Technical Report: IIIT/TR/2008/132, 2008. [online] Dostupné z www:
http://www.cse.iitb.ac.in/~comad/2008/PDFs/61-ankita.pdf
[5] Bar-Hilel, A., Hertz, T., Shental, N., Weinshall, D.; Learning distance functions using equivalence, Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington DC, 2003.
Tento web site byl vytvořen prostřednictvím phpRS - redakčního systému napsaného v PHP jazyce.
Na této stránce použité názvy programových produktů, firem apod. mohou být ochrannými známkami
nebo registrovanými ochrannými známkami příslušných vlastníků.