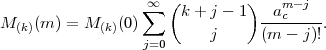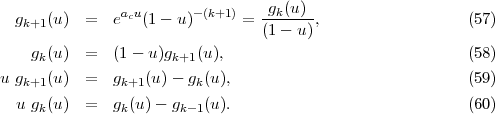Rozptyl provozního zatížení odmítnutého z obousměrného svazku

Autor: O. Hudousek <hudouso(at)fel.cvut.cz>, Pracoviště: České vysoké učení technické v Praze, FEL, Téma: Optimalizace, Vydáno dne: 10. 05. 2008
V příspěvku je provedeno odvození zobecněného vztahu pro výpočet rozptylu odmítnutého provozního zatížení použitelného pro přelivové toky z obousměrných svazků. Předpokládá se, že je obsluhovému systému nabízeno několik navzájem nezávislých toků provozního zatížení.

Abstract

The contribution is focused on the derivation of general equation that evaluates the variance of refused traffic. The resulting equation is valid in all cases, where the service system is being offered multiple traffic flows of the type PCT1. It allows determination of the variance of the flow formed by demands coming from one flow. Equations for evaluation of the variance of the traffic rejected from unidirectional and bidirectional trunks are only special cases of the derived formula. At the end of the contribution the result is verified by simulation.

1 Úvod

Telekomunikační síť se spojováním okruhů může být za jistých předpokladů modelována jako soustava obsluhových systémů M/M/N/0 dle Kendallovy klasifikace. Při dimenzování sítí s přelivem se často používá Wilkinsonova dvouparametrová metoda publikovaná v [1]. K jejímu použití je nutné stanovit rozptyl odmítnutého provozního zatížení pomocí vztahu:

           (1)

kde a je střední hodnota provozního zatížení nabízeného svazku,

x počet obsluhových linek,

m střední hodnota odmítnutého provozního zatížení,

v rozptyl odmítnutého provozního zatížení.

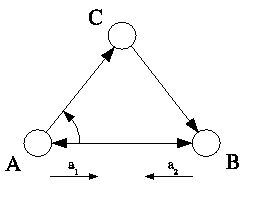
Tento vztah je přímo použitelný pro výpočet provozního zatížení odmítnutého z jednosměrného svazku. Složitějším případem je ovšem výpočet rozptylu provozního zatížení odmítnutého obousměrným svazkem, viz obr.1.

Obrázek 1: Obousměrný svazek mezi uzly A a B s přelivem v uzlu A.

Předpokládejme, bez větší újmy na praktické použitelnosti, že nabídky provozního zatížení z uzlu A do uzlu B (a1) a z uzlu B do uzlu A (a2) jsou navzájem nezávislé. Obousměrný svazek je potom možné popsat jako obsluhový systém, jemuž je nabízeno provozní zatížení ac = a1 + a2. Na rozdíl od jednosměrného svazku je však v tomto případě nutné uvažovat dva odmítnuté toky provozního zatížení. Jeden je tvořen odmítnutými požadavky, jež byly součástí toku a1, a druhý požadavky pocházejícími z nabízeného toku a2. Pro tento případ ovšem vztah 1 není použitelný.

Obsahem tohoto článku je odvození zobecněného vztahu pro výpočet rozptylu odmítnutého provozního zatížení. Výsledný vztah postihuje všechny případy, kdy je obsluhovému systému nabízeno více toků provozního zatížení typu PCT1 a je třeba stanovit rozptyl části odmítnutého provozního zatížení tvořené požadavky, jež byly součástí pouze jednoho z nabízených toků. Vztahy pro výpočet rozptylu odmítnutého zatížení z jednosměrných a obousměrných svazků jsou pak speciálním případem odvozeného vztahu. Uvedené odvození je zobecněním postupu uvedeného v [1], a proto je značení proměnných pro zjednodušení porovnání ponecháno ve shodě s původním textem.

2 Popis systémů s přelivem provozního zatížení

Odvození vztahu pro rozptyl odmítnutého zatížení vychází z popisu obsluhového systému pomocí Markovských řetězců. Pakliže zkoumáme pouze vlastnosti přímého toku provozního zatížení, může se obsluhový systém nacházet v x + 1 stavech, kde x je počet obsluhových linek. Intenzita přechodu mezi stavy m a m + 1 je pak λm a mezi stavy m a m - 1 je μm, přičemž ze stavu 0 může systém přejít pouze do stavu 1 a ze stavu N pouze do stavu N - 1. Jiné přechody nejsou možné. Vzhledem k tomu, že se předpokládá nabízený tok provozního zatížení typu PCT1, platí λm = λ pro m < N a μm = m · μ, kde λ je intenzita příchodů požadavků nabízených systému a μ intenzita obsluhy jedné obsluhové linky.

Pokud jsou ovšem předmětem zájmu také vlastnosti odmítnutého toku provozního zatížení, popisuje se systém jako soustava dvou svazků, přímého o N obsluhových linkách a (fiktivního) přelivového s obsluhových linek. Stavy systému jsou pak popisovány uspořádanou dvojicí (m,n), kde m je počet obsazených obsluhových linek přímého svazku a n přelivového svazku. Intenzity přechodů ze stavu (m,n) do stavu (m + 1,n) a z (m,n) do (m - 1,n) jsou totožné s předchozím případem. Navíc ovšem, předpokládáme-li stejnou intenzitu obsluhy μ obsluhových linek přímého i přelivového svazku, systém přechází ze stavů (m,n) do stavů (m,n - 1) (pro n > 0) s intenzitou μ. Tento přechod odpovídá uvolnění obsluhové linky v přelivovém svazku. Pokud je systém ve stavu (x,n), tj. jsou obsazeny všechny obsluhové linky přímého svazku, přechází s intenzitou λ do stavu (x,n + 1). Ze soustavy rovnic popisujících přechody mezi stavy systému lze pak stanovit i rozptyl provozního zatížení přeneseného přelivovým svazkem, jak bylo provedeno J.Riordanem v [1].

Úplný popis obousměrného svazku jako systému s jedním nabízeným tokem provozního zatížení, který se skládá ze dvou nezávislých toků a1 a a2, a dvěma toky odmítnutého provozního zatížení by pak vyžadoval popis pomocí "třírozměrného řetězce". Jednotlivé stavy by byly popsány uspořádanou trojicí čísel (m,n,o). Cílem této práce je však odvození vztahu pro rozptyl jednoho z odmítnutých toků provozního zatížení, a tak je možné vyhnout se úplnému popisu systému. Zkoumáme-li požadavky z nabízeného toku a1 odmítnuté přímým svazkem, pak již není nutné zabývat se odmítnutými požadavky pocházejícími z toku a2. Popis systému je pak obdobný jako v předchozím případě s tím rozdílem, že intenzita přechodu ze stavu (m,n) do stavu (m + 1,n) je, za předpokladu nezávislosti nabízených toků provozního zatížení, rovna součtu dílčích intenzit λc = λ1 + λ2, kde λ1, resp. λ2 jsou intenzity příchodů požadavků toků a1 a a2 (pozn. v dalším ac = a1 + a2), viz obr.2. Odvozený vzorec je potom možné použít pro výpočet rozptylu toku odmítnutých požadavků, které pocházejí z jednoho nabízeného toku provozního zatížení, přičemž nabízen může být libovolný počet toků provozního zatížení, pakliže jsou navzájem nezávislé.

Obrázek 2: Uspořádání stavů systému a intenzit přechodů mezi nimi.

3 Odvození zobecněného vztahu pro rozptyl odmítnutého provozního zatížení

Uvedený systém lze popsat soustavou rovnic pro m < x

           (2)

          (3)

a pro m = x

           (4)

          (5)

Tedy po úpravě a zavedení označení a1 = λ1 / μ a ac = (λ1 + λ2) / μ

           (6)

          (7)

          (8)

          (9)

K funkci f(m,n) je možné definovat její faktor moment:

           (10)

kde

           (11)

(n)0 = 1 a (n)k<0 = 0. Dále k tomuto momentu zavedeme exponenciální generující funkci

           (12)

pro níž platí

           (13)

          (14)

Dále platí, že

           (15)

a také

           (16)

Užitím těchto vztahů je možné upravit rovnice (8) a (9) do tvaru

           (17)

          (18)

Po úpravě tedy dostáváme

           (19)

          (20)

Pro výše definovanou moment generující funkci platí

           (21)

          (22)

Užitím těchto vztahů tedy můžeme psát

           (23)

a

           (24)

Budiž zavedena následující obecná generující funkce:

           (25)

pro kterou platí

Využitím těchto vztahů
          (31)

          (32)

Dále se řeší diferenciální rovnice:

Vzhledem k tomu, že pro obecnou generující funkci
          (38)

platí a(0) = A(0), je určena konstanta c:

           (39)

Dále se postupuje rozvojem řešení diferenciální rovnice do řad tak, aby bylo možné stanovit funkci M(k)(m) odpovídající obecné generující funkci Gk(u). Nejprve budiž stanoven rozvoj funkce f(u) = (1 - u)-k v Maclaurinovu řadu:

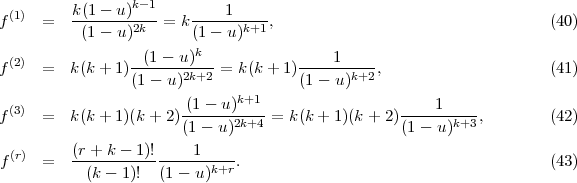
Příslušná Maclaurinova řada je tedy
          (44)

Obecnou generující funkci Gk(u) můžeme tedy vyjádřit pomocí rozvoje v řady jako

Z toho tedy plyne, že
          (51)

Pro G0(u) platí

           (52)

a tedy platí

           (53)

Dále se zavede označení

           (54)

pro σ0(m) platí:

           (55)

Dále se k posloupnosti σk(m) zavede obecná generující funkce

           (56)

Z toho lze odvodit rekurentní vztahy

Dále platí
          (61)

          (62)

Potom tedy

           (63)

          (64)

Pro obecnou generující funkci gk(u) platí:

Použitím vztahů (58) a (64) dostáváme
          (69)

          (70)

První z těchto vztahů se dá vyjádřit ve tvaru

           (71)

Druhý vztah (70) se dá přeuspořádat do tvaru, který bude vhodný pro další postup:

           (72)

Z druhého vztahu a z (9) plyne

           (73)

          (74)

Též platí

           (75)

          (76)

          (77)

          (78)

Dále iterací

Vzhledem k tomu, že
          (83)

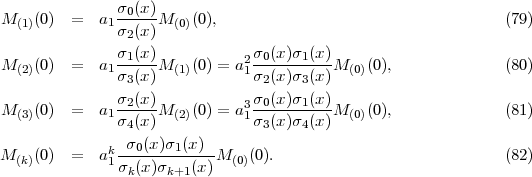
platí

           (84)

a tedy

           (85)

          (86)

a tedy konečně

           (87)

Pro samotné faktor momenty dostáváme vztah:

           (88)

          (89)

Mezi k-tým obecným momentem mk

           (90)

a k-tým faktor momentem Mk

           (91)

platí následující vztahy

konkrétně tedy
a výsledné momenty mk =Σ xm=0 mk(m) jsou
Dále využitím vztahu
          (103)

dostáváme

           (104)

          (105)

Označme celkový tok odmítnutého provozního zatížení mc:

           (106)

kde E1,x(a) je první Erlangova funkce, a můžeme pak psát

           (107)

Pro hledaný druhý centrální moment v2 tedy platí

           (108)

4 Ověření platnosti vztahu simulací

Platnost vztahu byla ověřena simulací časově věrnou metodou pro vybrané dvojice středních hodnot nabízených vstupních toků a1 a a2. Stavy systému (počty obsazených obsluhových linek) byly zjišťovány vzorkováním v pevných intervalech. Parametry volené shodně pro všechny simulace byly:

délka jednoho simulačního úseku tsim = 50 h,

počet simulačních úseků nsim = 200,

interval vzorkování tvz = 1, 2 s,

střední doba obsluhy tos = 120 s,

počet obsluhových linek x = 30.

V následující tabulce jsou srovnány výsledky simulace s výpočty dle odvozeného vztahu. K výsledkům simulace jsou uvedeny též meze 95-procentního konfidenčního intervalu td a th. B značí ztrátu, Vvyp značí hodnotu rozptylu vypočtenou odvozeným vztahem, Vsim hodnotu rozptylu stanovenou simulací. Ostatní symboly mají výše definovaný význam.

a1 [Erl] ac [Erl] B V vyp [Erl2] V sim [Erl2] td th
9 20 0,00845 0,13166 0,13169 0,12653 0,13685
11 20 0,00845 0,17600 0,17724 0,17057 0,18391
3 21 0,01359 0,05101 0,05056 0,04872 0,05240
18 21 0,01359 0,61304 0,61538 0,59809 0,63266
13 28 0,09812 2,53369 2,54177 2,51157 2,57197
15 28 0,09812 3,14682 3,15608 3,12430 3,18787
20 43 0,34149 11,07288 11,04999 10,97453 11,12546
23 43 0,34149 13,46574 13,42674 13,34250 13,51098

5 Vlastnosti vztahu

Na obrázku 3 je ukázána závislost poměru rozptylu odmítnutého toku V a jeho střední hodnoty M na počtu vedení příčky N. V grafu jsou znázorněny průběhy pro různý poměr velikosti toku, který je odmítán odděleně a celkového toku. Z uvedeného vyplývá, že čím větší je celkový tok Ac v poměru proti toku A, tím menší je rozptyl odděleně odmítaného toku V .


Obrázek 3: Závislost poměru V/M na počtu vedení přímého svazku N.

6 Závěr

V této práci bylo provedeno odvození zobecněného vztahu pro výpočet rozptylu odmítnutého provozního zatížení, jenž mj. umožňuje výpočet tohoto rozptylu pro přelivové toky z obousměrných svazků. Předpokládá se, že je obsluhovému systému nabízeno několik navzájem nezávislých toků provozního zatížení. Pomocí odvozeného vztahu lze pak vyčíslit rozptyl toku odmítnutého provozního zatížení, jenž je tvořen požadavky, které pocházejí z jednoho z nabízených toků provozního zatížení:

           (109)

kde ac je součet všech toků provozního zatížení nabízených systému,

mc součet všech toků odmítnutého provozního zatížení,

a1 jeden z nabízených toků provozního zatížení,

m1 tok odmítnutého provozního zatížení tvořený požadavky z toku a1,

x počet obsluhových linek přímého svazku,

v rozptyl toku odmítnutého provozního zatížení m1.

Tento vztah lze následně použít pro dimenzování popsaných obsluhových systémů s přelivem Wilkinsonovou metodou, a tedy i pro dimenzování obousměrných svazků s přelivem.

Použitá literatura

[1] Wilkinson, Roger. I. Theories for toll traffic engineering in the U.S.A. The Bell System Technical Journal, 1956, vol.35, p.421514.