Výběr nejvhodnějšího konvolučního kódu - I

Při přenosu dat se díky zvyšování přenosové rychlosti stále častěji setkáváme s chybami, které mají tendenci shlukovat se. K dispozici jsou konvoluční kódy, které jsou schopny tento přenos dostatečně účinně zabezpečit. Budou srovnány základní konvoluční kódy, které jsou snadno obvodově řešitelné a lze tak jednodušeji simulovat jejich funkci. Předkládaný článek se zabývá návrhem příslušných kódů.

---

Selection of the optimal convolutional code - I.

Abstract

Because of increasing transfer rate during the data transmission errors, which have a tendency to flock in, appear more frequently. To use are available convolutional code, which are able to secure efficiently enough transmission. Comparison of basic convolutional codes, which have easy realization in basic logical circuits and thanks to that their functions simulation is simple, will be shown. This paper defines proposal of relevant codes.

---

Poprvé byly představeny konvoluční kódy pro opravu shlukových chyb Hagelbargerem. Dále pak nezávisle na sobě Iwadari a Masery zkonstruovali efektivnější kódy stejného typu. Jejich kódy se stejnou korekční schopností vyžadují kratší ochranné intervaly než Hagelbargerovy kódy. Optimální kódy pro opravu postupných shlukových chyb byly později objeveny nezávisle Berlekampem a Preparatem.

Pro výše uvedené systematické konvoluční kódy bude ukázán návrh kodéru a dekodéru, který je schopen opravit shluk 4 chyb. Díky systematičnosti ve výsledné přenášené kódové kombinaci lze vždy rozlišit prvky informační a zabezpečující. Jednotlivé kódy jsou popsány především vytvářecí blokovou maticí B, pomocí níž lze odvodit jednotlivé prvky kodéru i dekodéru a jejich následné potřebné zapojení. V dalším pokračování článku se navíc budeme zabývat nejlepší variantou mezi těmito kódy.

Při vytváření konvolučního kódu se nám nabízejí dvě základní metody. Kód lze zadat buď pomocí vytvářcího mnohočlenu nebo pomocí vytvářecí matice. U příjemce zprávy se pro nalezení nejpravděpodobnějšího odhadu správné posloupnosti používá u konvolučních kódů Viterbiho algoritmus. Princip algoritmu spočívá ve vyhledávání nejmenší Hammingovy vzdálenosti dekódované poslopnosti od přijaté posloupnosti. Nevýhodou zmiňovaného algoritmu je jeho značná náročnost na počet numerických operací. Uvedený způsob se používá jen pro dekódování kódů s relativně krátkými omezujícími délkami, jelikož závislost počtu prováděných operací má exponenciální charakter. Další metodou k vyhledávání chyb, která bude u jednotlivých kódů v tomto článku použita je princip prahového dekódování. Základním vlastností prahového dekódování je nalezení dostatečného počtu kontrolních operací mezi jednotlivými prvky úseku zprávy, které mají mezi sebou tzv. vztah ortogonality vzhledem k prvku, jehož správnost se po přenosu kontroluje.

Základní Hagelbargerův kód (n₀; n₀ - 1)

Kód lze určit pomocí blokové matice v dekadickém tvaru B_D, která má tvar čtvercové matice rozměru n₀ x n₀ a v každém řádku je v místě odpovídající prvku na úhlopříčce liché dekadické číslo. Řádky se číslují odspodu a v prvním řádku je trojka, v (n₀ - 1) řádku je (2n₀ - 1) poslední řádek obsahuje jedničku viz. (1).

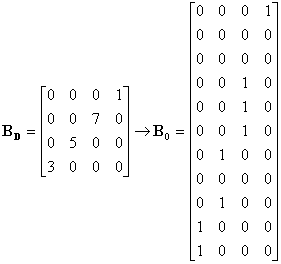(1)

Matice B_D se pro potřebu dvojkových kódů převádí na blokovou matici ve dvojkovém tvaru B₀. Dvojková bloková matice B₀ má opět n₀ sloupců. Počet řádků je určen součinem n₀ a počtem míst potřebných k zapsání největšího čísla, které se v B_D vyskytuje. Počet míst dekadického čísla n, potřebných pro jeho zapsání dvojkovým číslem, označujeme L(n), což je nejmenší celé číslo, které vyhovuje nerovnosti:

(2)

Dvojková čísla s menším počtem míst mají v matici B₀ na nepoužitých místech nuly. První číslo odspodu má vždy pouze dva řádky, protože nuly v místech nepoužitých dvojkových míst by způsobovaly v realizaci kodéru pouze neužitečné časové zpoždění. Pro počet řádků dvojkové matice jde tedy odvodit následující vztah:

(3)

Tento kód opravuje shluky chyb délky b bitů:

(4)

Mezi těmito shluky chyb musí být v bitovém toku bezchybný úsek – ochranný interval A:

(5)

Kód pro opravu shluku chyb b délky až 4 bity potřebuje dodržení ochranného intervalu A minimální délky 47 bitů. Vytvoření zapojení kodéru odvodíme z B₀ viz. (1) pomocí souboru vytvářecích mnohočlenů. U vytvářecího mnohočlenu je výstupním tokem čtvrtý sloupec blokové matice. Vstupním tokem je postupně první až třetí sloupec této matice. Hledají se řádky, kde se příslušné dva sloupce liší. Zapojení kodéru jest uvedeno na Obr. 1 a určují jej zabezpečující vytvářecí mnohočleny získané z vytvářecí blokové matice:

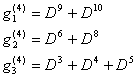(6, 7, 8)

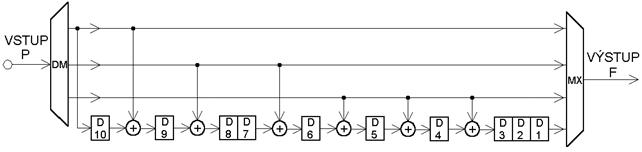
Obr. 1 - Kodér Hagelbargerova kódu pro korekci 4 chyb

Dekodér Hagelbargerova kódu vychází z obecného schématu dekodéru se syndromovým dekódováním (viz. Obr. 2). Využívá se přímého převodu vektoru syndromu na chybový vektor. Z přeneseného bloku dat se oddělí zabezpečovací prvek, který se sečte mod2 s nově vypočítaným zabezpečovacím prvkem, jenž se vytvořil v kodéru přijímače. Tím vznikne syndromový prvek s, který slouží k nalezení a korekci chyb v dílčích posloupnostech přenesených informačních prvků.

Obr. 2 - Dekodér Hagelbargerova kódu pro korekci 4 chyb

Základní Iwadari-Maseryův kód (m*n₀; m*k₀)

Iwadariho kód je opět popsán vytvářecí blokovou maticí B₀, která má n₀ sloupců. Sloupce jsou indexovány zleva od a_i, řádky se číslují vzestupně zespodu. Na nejvyšším řádku úplně vpravo je umístěna jednička představující zabezpečovací prvek. Následují nulové řádky až do počtu n₀. V dalším řádku je umístěna jednička posunutá oproti původní pozici o jedna doleva. Následující řádek má jedničku na stejné pozici. Takto je zajištěna oprava jednoho bitu. Pro opravu dalších je třeba se opět posunout o jednu pozici vlevo a počet vložených nulových řádků mezi dvěma jedničkami ve stejném sloupci vždy vzrůstá o jeden řádek až do celkové velikosti n₀. Názorně uvedeno v rovnici (9), kde je obecné schéma vytvářecí matice Iwadariho kódu.

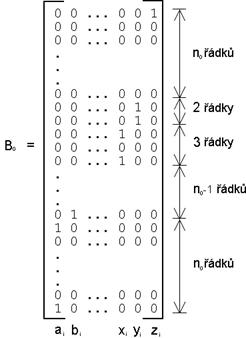(9)

Pro jednotlivé parametry kódu platí:

(10)

kde m a k₀ jsou definovány:

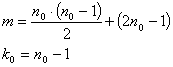(11, 12)

k₀ a n₀ představuje počet dílčích vstupních či výstupních paralelních toků. Při návrhu jsou třeba ještě parametry pro korekční schopnost b a ochranný interval A:

(13, 14)

V případě překročení mezní zabezpečovací schopnosti nezpůsobuje tento kód nekonečný průnik chyby do vlastní informace. Z vytvářecí blokové matice lze opět vytvořit kodek Iwadariho kódu viz Obr. 3 a 4. Vyjdeme z vytvářecí blokové matice B₀ určené ze vztahu (9). Pro vytvoření návrhu zapojení je důležitá syndromová rovnice matice kódu, z níž lze odvodit jednotlivé prvky kodéru. Za předpokladu, že v samotném kodéru nevznikají chyby pak pro zabezpečovací prvek d₁₃ platí:

(15)

Uvedená rovnice (15) přímo určuje schéma zapojení kodéru viz Obr. 3.

Obr. 3 - Kodér Iwadari-Maseryova kódu pro korekci 4 chyb

Způsob dekódování dat na straně příjemce je naznačen na Obr. 4. Princip dekodéru spočívá ve využití prahového dekódování. K syndromové rovnici pro určitý čas k bitům v ní obsažených je třeba nalézt bity na zabezpečení se podílejících v čase předcházejícím. Za pomocí dvou syndromových rovnic lze provést korekci jednoho bitu. Pro korekci dalších bitů je třeba jít dále „hlouběji do historie“ a určit tak další nezbytné syndromové rovnice. Jejich celkový počet určuje množství potřebných syndromových paměťových buněk. Model dekodéru (viz. Obr. 4.) je sestaven na základě znalostí potřebných rovnic:

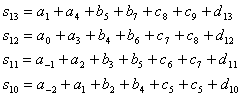(16, 17, 18, 19)

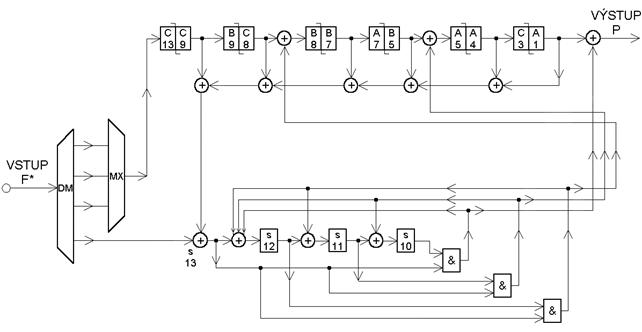
Obr. 4 - Dekodér Iwadari-Maseryova kódu pro korekci 4 chyb

Základní Berlekamp-Preparatův kód (n₀; n₀ - 1; m)

Postup objevený nezávisle Berlekampem a Preparatem, vždy přinese kód splňující Gallagerovy meze. Gallager ukázal, že libovolný konvoluční kód o informační rychlosti R má schopnost opravit všechny shluky délky b nebo kratší vzhledem k ochrannému intervalu délky A, jestliže platí:

(20)

Tento vztah je znám jako mez kompletní opravy shlukové chyby. Z tohoto důvodu jsou Berlekamp-Preparatovy kódy optimální pro opravu postupných shlukových chyb.

Jedná se o systematický konvoluční kód ke korekci shluků omezených do samostatného bloku úměrného ochranému intervalu m bezchybných bloků (tj. shluk může ovlivnit nanejvýš jeden blok omezené délky). Tento kód by měl mít schopnost postupné opravy shlukových chyb jednoho bloku úměrně ochrannému intervalu m bloků. I tento kód lze popsat vytvářecí maticí B₀, jejíž rozměry jsou n₀ x 2n₀, jež se skládá ze dvou podmatic. První podmatice má jedničky na vedlejší diagonále a druhá podmatice má nad hlavní diagonálou jedničky. Přičemž obě podmatice mají shodný rozměr n₀ x n₀. Zbylé prvky jsou nulové viz. (21).

(21)

Z (20) při podmínce R = (n₀ - 1)/n₀ dostaneme další parametry kódu:

(22)

Bloková vytvářecí matice určuje způsob zapojení kodéru viz. Obr 5. Opět se jedná o systematický konvoluční kód s generačními polynomy:

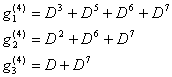(23, 24, 25)

Obr. 5 - Kodér Berlekamp-Preparatova kódu pro korekci 4 chyb

Berlekamp-Preparatovy kódy mohou být dekódovány použitím obecné dekódovací techniky pro konvoluční kódy opravující shlukové chyby zásluhou Masseyho. V uvedeném dekodéru nemůže nastat nekonečné šíření chyby a jeho schéma je uvedeno na Obr. 6.

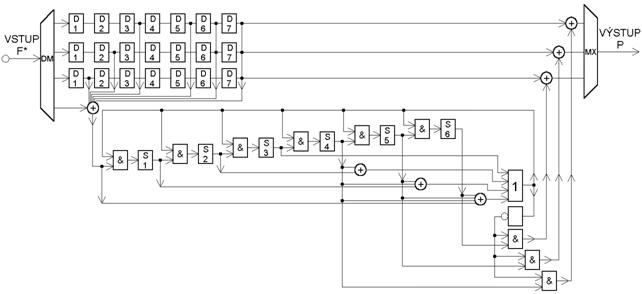
Obr. 6 - Dekodér Berlekamp-Preparatova kódu pro korekci 4 chyb

Závěr

Zabezpečení se dosahuje zvýšením nadbytečnosti na úkor vlastního přenosu užitečné informace. Je tedy velmi důležité najít nejvhodnější řešení, které se ovšem liší případ od případu. Zde uvedená řešení jsou srovnána v pokračování tohoto článku. Avšak chybovostí v systému se zabýváme, až pokud výskyt různých typů chyb překročí únosnou mez. Pomocí konvolučních kódů lze realizovat zabezpečení přenášené posloupnosti nepřetržitým způsobem. Nejpoužívanější typy kódů z této skupiny představují ochranu před shluky chyb různé délky. Druhý díl článku.

Tento článek vznikl za podpory výzkumného projektu FRVŠ - 993 G1 "Simulace zabezpečovacích korekčních kódů a její začlenění do výuky předmětu Datová komunikace".

Literatura

[1] Křivánek, V., Číka, P.: Simulace shlukových chyb v Matlabu. Elektrorevue, 2006, č. 35, str. 1-10. ISSN 1213-1539.
[2] Křivánek, V.: Verification of the Error-Control Security Process by Means of Simulation. International Transactions on Communication and Signal Processing, 2006, vol. 9, no. 1, p. 128-136, ISSN: 1738-9682.
[3] Němec, K.: Kódové zabezpečovací systémy. Teze habilitační práce, ÚTKO FEI VUT Brno, Brno 1999, 34s., ISBN 80-214-1312-3.
[4] Němec, K.: Výběr optimálního protichybového kódu. Elektrorevue, 2006, č. 54., str. 1-9. ISSN 1213-1539.
[5] Shu, L.; Costello, D.: Error Control Coding – Fundamentals and Applications. Prentice-Hall, Inc., Englewood Cliffs, New Jersey 1983, 603 p., ISBN 0-13-283796-X.