Algoritmus detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měření
Autor: L. Chmela, P. Novák, J. Burčík <chmellad(at)fel.cvut.cz>, Pracoviště: České vysoké učení technické v Praze, FEL, Téma: Digitální zpracování signálu, Vydáno dne: 08. 09. 2012Algorithm for Detection and Elimination of the Negative Impact of Radio Relay Links on the Meteorological Radar Measurement Including The Use of Knowledge of Previous Results
The paper presents a new algorithm for detection and elimination of a negative impact of radio relay links on the meteorological radar measurement based on the application of image processing methods using the information from the previous radar processing.
Keywords: Meteorological Radar Measurement; Radar Images; Digital Signal Processing; Image Processing
Úvod
Počasí ovlivňuje téměř každou lidskou činnost, ať jde o jedince či o společnost, o osobní život či o práci. Znalost aktuálního stavu meteorologických podmínek a schopnost předpovědi jejich vývoje umožňuje využívat efektivněji jak času, tak prostředků při činnosti závislé na počasí. Výhodou je, pokud jsou meteorologické podmínky vyhodnocovány automaticky, neboť se tím umožní autonomní chod monitorovacích a vyhodnocovacích systémů.
Navazujeme na předchozí řešení této problematiky [1], kdy již byly popsány různé zdroje meteorologických informací, ať jde o nejjednodušší teploměry, sofistikované meteorologické stanice, satelitní snímání atmosféry, radiolokační měření srážkové oblačnosti či např. vizuální monitorování oblohy na meteorologických stanicích. Automatické vyhodnocování číselných údajů (např. teploty) je v zásadě jednoduché, neboť jde většinou o sledování překročení určitých limitních hodnot, případně doplněné o kombinaci jednoduchých početních operací. Ovšem automatické vyhodnocování meteorologických dat obrazového charakteru [2] již s sebou přináší řadu komplikací, neboť obrazová data jsou velice rozmanitá a automaticky odhalit případné chyby v nich vyžaduje složitější (inteligentní) algoritmy. Jednou z takovýchto komplikací je negativní vliv radioreléových spojů na meteorologická radarová měření [3, 4]. Tento negativní vliv se projeví vnesením chyb do dat změřených radiolokátory a potažmo zanesením falešných cílů do radarových snímků. V současnosti je v ČR operativně používán algoritmus na eliminaci rušivých informací z radarových dat [4], který se snažíme inovovat.
V tomto článku představujeme nový algoritmus detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měření založený na aplikaci metod zpracování obrazu s využitím informací ze zpracování časově předchozích radarových dat (pracovní název algoritmu je LASTx, kde x udává, kolik časově předchozích radarových dat je do algoritmu zahrnuto – v článku 0 až 6, tedy LAST0 až LAST6). Cílem tohoto článku je porovnat výsledky vyvinutého algoritmu LASTx se stávajícím algoritmem ČHMÚ a navrhnout optimální počet vyhodnocovaných dat.
Materiál a metody
Zkoumaným materiálem popisovaným níže jsou produkty meteorologických radarových měření. Soubor testovaných dat je tvořen 36 archivovanými naměřenými radarovými daty – radarovými snímky. Soubor je tvořen 36 snímky pořízenými v pětiminutových intervalech mezi 13:04 a 15:59 UTC dne 10.12.2009. Níže také popisujeme metody zpracování obrazů využité při zpracování radarových dat. Uvádíme postup detekce negativního vlivu radioreléových spojů na měření meteorologických radarů za použití Houghovy transformace i postup eliminace detekovaného negativního vlivu radioreléových spojů na měření meteorologických radarů s využitím informací ze zpracování časově předchozích radarových dat. Dále uvádíme metodiku hodnocení úspěšnosti detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měření a metodiku statistického posouzení významnosti rozdílů v hodnocení úspěšnosti algoritmu ČHMÚ a algoritmu LASTx.
Meteorologická radarová měření a jejich produktyMeteorologické radary slouží k detekci srážkové oblačnosti na velké ploše (dosah cca 250 km) a identifikaci konvektivních bouří, se kterými souvisí množství nebezpečných meteorologických jevů (přívalové srážky, nárazy větru, kroupy, blesky). Radarová měření jsou v kombinaci s údaji ze srážkoměrů používána k detailní analýze prostorového rozložení srážkových úhrnů a jejich předpovědi na několik nejbližších hodin. Princip funkce radaru je založen na zpětném rozptylu mikrovln (vlnová délka jednotky cm) na vodních kapkách a ledových krystalcích ve srážkách a oblačnosti. V České republice využívá celoplošně meteorologických radiolokátorů Český hydrometeorologický ústav (ČHMÚ), jehož radarové oddělení [7] obhospodařuje v současnosti dva meteorologické dopplerovské radiolokátory pracující v pásmu C (vlnová délka 5 cm): pro východní část ČR a okolí radar na kótě Skalky na Drahanské vrchovině a pro západní část ČR a okolí radar na kótě Praha na Brdské vrchovině.
Meteorologická měření se obvykle skládají z cca 10 až 20 otáček antény v azimutu s proměnným výškovým úhlem (elevací). V případě českých radarů jsou měření na 12 různých elevacích opakována každých 5 minut [7]. Objemová radarová data ve sférických souřadnicích jsou ukládána do souborů v interním formátu RVD (otevřený formát nezávislý na výrobci radaru) [8]. Objemová data jsou zapisována po jednotlivých elevacích a každá elevace se skládá z paprsků s pevným azimutálním krokem 1º. Data jsou zapisována paprsek po paprsku ve směru pohybu hodinových ručiček. Každý paprsek je zapisován směrem od radaru k maximální vzdálenosti. Každá hodnota (sférický pixel) je zapsána pomocí 1 bytu (8 bitů). Data jsou kódována dle SIGMET RVP6 konvence (0 se používá pro neměřitelnou hodnotu (příliš nízký přijatý signál nebo vymazaný nemeteorologický cíl), 1 představuje nejnižší kódovanou radiolokační odrazivost –31,5 dBZ, rozlišení hodnot odrazivosti je 0,5 dBZ). Obr. 1 ilustruje data jako obrazovou informaci v tzv. B-display [8]. Jedná se o znázornění radarové odrazivosti Z pro nejnižší elevaci (θ = 0,1º).
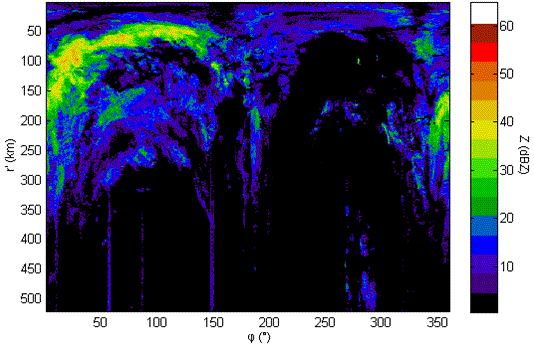
Obr. 1 Orientační znázornění odrazivosti Z pro nejnižší elevaci ve sférických souřadnicích.
Radarová data se pro praktické použití převádějí ze sférických souřadnic (r, θ, φ) do 3D kartézských souřadnic (x, y, z). Na obr. 2 je znázorněna stejná situace jako na obr. 1, tentokrát ale v kartézských souřadnicích, v tzv. PPI-display (PPI: Plan-position indicator) [9]. Toto znázornění lze již lehce použít např. na propojení s mapovým podkladem pro geografickou lokalizaci detekované srážkové oblačnosti.
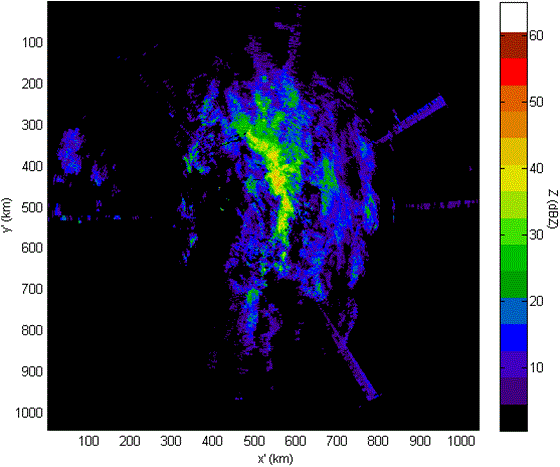
Obr. 2 Orientační znázornění odrazivosti Z pro nejnižší elevaci v kartézských souřadnicích.
Pro naše účely však budeme využívat zobrazení ve sférických souřadnicích, neboť negativní vliv radioreléových spojů je v takovém obraze snáze identifikovatelný. Radioreléové spoje operují na shodném kmitočtu (v pásmu 5 GHz) jako meteorologické radiolokátory a způsobují nežádoucí interference na snímcích radiolokační odrazivosti [3, 4]. Meteorologické radiolokátory mají natolik citlivé přijímače, že zachytí i velmi vzdálené radioreléové komunikace. Podobně jako slabá interference RLAN se může též projevit detekce slunečního záření (dochází k tomu však pouze občas při východu či západu slunce). Interference se na radarových snímcích projevují jako paprskovité útvary ve směru zdroje rušení, směrem od ovlivněného radaru (viz obr. 1 a 2) [7]. V současnosti ČHMÚ operativně používá algoritmus na eliminaci tohoto negativního vlivu, který je schopen částečně tento negativní vliv odstranit [4]. Tento algoritmus zpracovává radarová data paprsek po paprsku (azimut po azimutu) a sleduje aktuální hodnoty odrazivosti ve vztahu k situaci v nejbližších sousedních paprscích (sleduje četnost dostatečně silného oboustranného gradientu v rámci daného paprsku). Náš přístup je obdobný, ale vychází z algoritmů pro zpracování obrazu, zejména detekce hran [6] a Houghovy transformace [5], a dále využívá při zpracování aktuálních radarových dat informací ze zpracování časově předchozích dat.
Soubor testovaných dat je tvořen archivovanými naměřenými radarovými daty (bez aplikovaného eliminačního algoritmu ČHMÚ) po dobu tří hodin dne 10.12.2009. Soubor je tvořen 36 snímky pořízenými v pětiminutových intervalech mezi 13:04 a 15:59 a byl vybrán pro tento článek záměrně, neboť obsahuje množství chyb v rozsáhlé, ale nestejnorodé srážkové oblačnosti. Při takové situaci se negativní vliv radioreléových spojů na měření meteorologických radarů velmi obtížně detekuje a mohou se snáze odhalit slabiny testovaných algoritmů.
Metody zpracování obrazů využité při zpracování radarových datV předchozí studii [5] jsme pojednali o problematice detekce negativního vlivu radioreléových spojů na měření meteorologických radarů za použití metod zpracování obrazu [10, 11, 12], kde jako hlavní nástroj byla vybrána Houghova transformace, neboť hledaný negativní vliv radioreléových spojů se v radarovém obraze jeví jako liniový objekt. Jednou z operací tohoto postupu je rovněž detekce hran ve fázi přípravy obrazu pro aplikaci Houghovy transformace. Ukázalo se [6], že hranové detektory využívající operátory Sobelův, Prewittové a Robertsův způsobí nemožnost identifikace hledaného rušení v silně zašuměných oblastech, naopak tuto schopnost prokázaly hranové detektory Canny, LoG a Zero-Crossing. V případě použití Cannyho operátoru však detekce hran trvá dvojnásobný čas, což může být limitující při požadavcích na zpracování v co nejkratším čase. V našem algoritmu jsme využili Marr-Hildrethův detektor založený na 2. derivaci (Zero-Crossing), neboť výsledky detekce liniových chyb vykazovaly spojitější objekty než při využití operátoru Laplacián Gaussiánu (LoG).
Postup detekce negativního vlivu radioreléových spojů na měření meteorologických radarů za použití Houghovy transformace se děje v zásadě podle těchto kroků:
1) konverze radarového snímku na binární obraz,
2) úprava obrazu pro následnou detekci (operace matematické morfologie, především uzavření),
3) detekování hran (Zero-Crossing),
4) detekování liniových objektů (Houghova transformace),
5) úprava a spojení detekovaných liniových objektů (linií),
6) skenování původního radarového obrazu v okolí detekovaných linií (přechod od liniové hrany k objektu – rušivému paprsku),
7) zobrazení výsledků detekce v originálním radarovém snímku.
Postup eliminace detekovaného negativního vlivu radioreléových spojů na měření meteorologických radarů s využitím informací ze zpracování časově předchozích radarových dat se děje v zásadě podle těchto kroků:
1) skenování původního radarového obrazu v okolí linií detekovaných v x časově předchozích obrazech (využití informací z x předcházejících radarových měření uskutečněných po 5 minutách),
2) nahrazení hodnot detekovaného rušení dopočítanými hodnotami odrazivosti (interpolace z hodnot okolí),
3) zobrazení výsledků eliminace v originálním radarovém snímku.
Metodika hodnocení detekce negativního vlivu radioreléových spojů na meteorologická radarová měření je založena na komparaci detekovaných chyb lidským okem a počítačovým algoritmem. Hodnotíme pro každý snímek výsledky detekce stávajícím algoritmem ČHMÚ a námi vyvinutým algoritmem LASTx. Přitom se odlišuje těchto 5 typů chyb:
A) Okem pozorovatelná chyba jako souvislé liniové rušení, četnost NA, významnost kA = 1.
B) Okem pozorovatelná chyba jako rušení v přerušované linii, četnost NB, významnost kB = 0,5.
C) Chyba nepozorovaná okem, ale detekovaná algoritmem, s pozitivním dopadem, četnost NC, významnost kC = 0,25.
D) Chyba nepozorovaná okem, ale detekovaná algoritmem, s neutrálním dopadem, četnost ND, významnost kD = –0,25.
E) Chyba detekovaná algoritmem s negativním dopadem (vyhodnocován jen celkový počet na všechny vzorky).
Chyba typu E, detekovaná algoritmem s negativním dopadem, je nepřístupná a její četnost musí být nulová.
Hodnocení úspěšnosti detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měření je prováděno jak hodnocením rozdílu v úspěšnosti detekování jednotlivých druhů chyb (resp. chyb typu A a B), tak hodnocením rozdílu v přepočtené četnosti detekovaných chyb. Výpočet přepočtené četnosti detekovaných chyb využívá již zmíněných koeficientů významnosti kA až kD a výsledná hodnota je tak ovlivněna váhou významnosti typů detekovaných chyb. Přepočtená četnost okem pozorovatelných chyb typu A a B se vypočítá podle rovnice (1). Přepočtená četnost chyb typu A a B detekovaných algoritmem ČHMÚ se vypočítá podle rovnice (2). Přepočtená četnost chyb typu A a B detekovaných algoritmem LASTx se vypočítá podle rovnice (3). Přepočtená četnost chyb typu A a B i C a D detekovaných algoritmem LASTx se vypočítá podle rovnice (4).
| NAB = NA·kA + NB·kB | (1) |
| NABč = NAč·kA + NBč·kB | (2) |
| NABx = NAx·kA + NBx·kB | (3) |
| NABx+ = NAx·kA + NBx·kB + NCx·kC + NDx·kD | (4) |
Pro hodnocení rozdílu v úspěšnosti detekování jednotlivých druhů chyb (resp. chyb typu A a B) je potřeba vypočítat procentuální úspěšnost přepočtených četností chyb detekovaných algoritmy ČHMÚ a LASTx ku přepočtené četnosti okem pozorovatelných chyb, jak ukazují rovnice (5) až (11).
| PNAč = 100·NAč / NA | (5) |
| PNBč = 100·NBč / NB | (6) |
| PNABč = 100·NABč / NAB | (7) |
| PNAx = 100·NAx / NA | (8) |
| PNBx = 100·NBx / NB | (9) |
| PNABx = 100·NABx / NAB | (10) |
| PNABx+ = 100·NABx+ / NAB | (11) |
Pro statistické posouzení významnosti rozdílů v hodnocení úspěšnosti algoritmu ČHMÚ a algoritmu LASTx jsme stanovili následující nulovou hypotézu H0: Mezi úspěšností algoritmu ČHMÚ a úspěšností algoritmu LASTx není rozdíl. Alternativní hypotéza je potom HA: Úspěšnost algoritmu LASTx je jiná (lepší) než úspěšnost algoritmu ČHMÚ.
Ze známých statistických metod [13, 14, 15] jsme pro náš případ zvolili párový t-test, neboť se jedná o analýzu výsledků dvou algoritmů na identických vzorcích dat. Směrodatnou chybu spočítáme podle vzorce (12), kde di představuje rozdíl NAx – NAč, resp. NBx – NBč, resp. NABx – NABč, resp. NABx+ – NABč. Testovací statistika má tvar (13). Jelikož máme n = 36 testovacích párů, stupeň volnosti je n – 1 = 35.
|
| (12) |
|
| (13) |
Výsledky
Výsledky uvedeny níže jsou tvořeny grafickým znázorněním vyhodnocení úspěšnosti detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měření, tabulkovým souhrnem četností jednotlivých typů chyb a vypočtených úspěšností algoritmů a statistickým zpracováním výsledků.
Grafické znázornění vyhodnocení úspěšnosti detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měřeníNa následujících obr. 3 až obr. 5 je graficky znázorněno vyhodnocení úspěšnosti detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měření pro jeden vybraný radarový snímek v čase 13:14 ze sledované série 36 snímků ze dne 10.12.2009. Pro LASTx je vybrána varianta zahrnutí 4 časově předchozích radarových dat – jde tedy o algoritmus LAST4. Pro ilustraci jsou znázorněny původní snímek s vyznačením okem pozorovatelných chyb (obr. 3), snímek s vyznačenými chybami detekovanými algoritmy ČHMÚ a LAST4 (obr. 4) a výsledný snímek po eliminaci chyb algoritmy ČHMÚ a LAST4 (obr. 5).
Na obr. 3 je originální snímek pro čas 13:14 s vyznačením NA = 7 okem pozorovatelných chyb jako souvislé liniové rušení (symbol červené šipky s kolečkem) a NB = 1 okem pozorovatelných chyb jako rušení v přerušované linii (symbol zelené šipky). Na obr. 4 vlevo je znázorněno detekování algoritmem ČHMÚ NAč = 2 okem pozorovatelných chyb jako souvislé liniové rušení a NBč = 0 okem pozorovatelných chyb jako rušení v přerušované linii. Na obr. 4 vpravo je znázorněno detekování algoritmem LAST4 NA4 = 7 okem pozorovatelných chyb jako souvislé liniové rušení, NB4 = 1 okem pozorovatelných chyb jako rušení v přerušované linii, NC4 = 1 chyb nepozorovatelných okem, ale detekovaných algoritmem, s pozitivním dopadem (symbol fialové šipky se znaménkem +) a ND4 = 1 chyb nepozorovaných okem, ale detekovaných algoritmem, s neutrálním dopadem (symbol černé šipky se znaménkem –). Na obr. 5 jsou výsledné snímky ze 13:14 po eliminaci chyb algoritmy ČHMÚ (vlevo) a LAST4 (vpravo).

Obr. 3 Okem pozorovatelné chyby ve snímku ze 13:14.
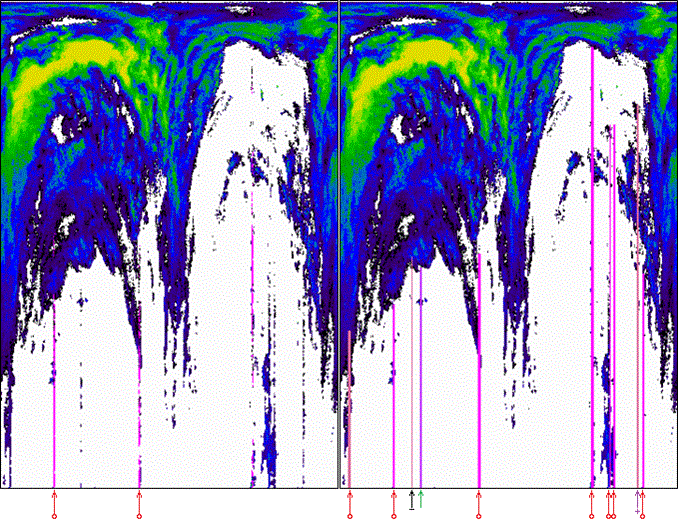
Obr. 4 Chyby detekované ve snímku ze 13:14 algoritmem ČHMÚ (vlevo) a algoritmem LAST4 (vpravo).
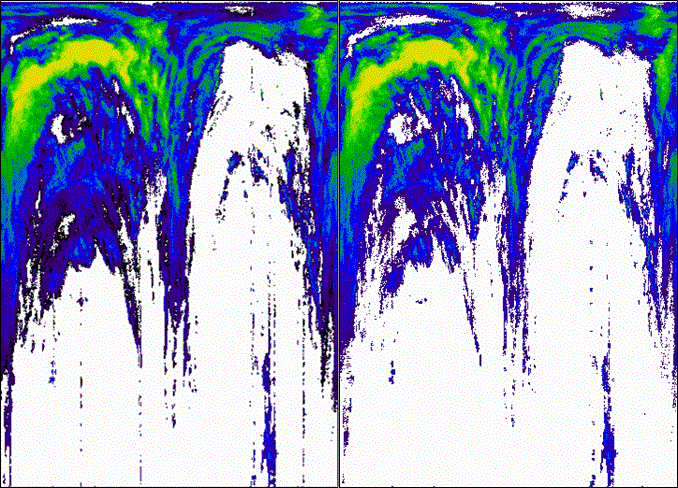
Obr. 5 Chyby detekované ve snímku ze 13:14 algoritmem ČHMÚ (vlevo) a algoritmem LAST4 (vpravo).
Četnosti jednotlivých typů chyb a vypočtené úspěšnosti algoritmůV tab. 1 jsou uvedeny četnosti okem pozorovatelných chyb typu A (souvislé liniové rušení) a B (rušení v přerušované linii) v původních datech (NA a NB) a detekovaných algoritmem ČHMÚ (NAč a NBč) a algoritmem LAST4 (NA4 a NB4) a četnosti chyb nepozorovaných okem, ale detekovaných algoritmem, typu C (s pozitivním dopadem) a D (s neutrálním dopadem) detekovaných algoritmem LAST4 (NC4 a ND4). Z těchto četností jsou v tab. 1 uvedeny přepočítané četnosti NAB podle vzorce (1), NABč podle vzorce (2), NAB4 podle vzorce (3) a NAB4+ (LAST4+) podle vzorce (4). Z jednotlivých četností jsou vypočítány aritmetické průměry a uvedeny v posledním řádku tab. 1. Průměrná přepočtená četnost okem pozorovatelných chyb typu A a B je pro původní data 6,3, pro výsledky algoritmu ČHMÚ 3,2, pro výsledky algoritmu LAST4 5,0 a s připočtením chyb nepozorovaných okem typu C a D (LAST4+) 5,1. Stejným způsobem obsahuje kompletní tabulka dat všechny varianty LASTx: LAST0 až LAST6.
| algoritmus → | původní data | ČHMÚ | ... | LAST4 | LAST4+ | ... | ||||||||
| čas měření ↓ | NA | NB | NAB | NAč | NBč | NABč | ... | NA4 | NB4 | NAB4 | NC4 | ND4 | NAB+ | ... |
| 01) 13:04 | 7 | 9 | 9,5 | 6 | 0 | 6,0 | ... | 6 | 0 | 6,0 | 0 | 0 | 6,0 | ... |
| 02) 13:09 | 5 | 3 | 6,5 | 3 | 0 | 3,0 | ... | 5 | 2 | 6,0 | 2 | 0 | 6,5 | ... |
| 03) 13:14 | 7 | 1 | 7,5 | 2 | 0 | 2,0 | ... | 7 | 1 | 7,5 | 1 | 1 | 7,5 | ... |
| 04) 13:19 | 7 | 0 | 7,0 | 5 | 0 | 5,0 | ... | 7 | 0 | 7,0 | 3 | 0 | 7,8 | ... |
| 05) 13:24 | 5 | 3 | 6,5 | 3 | 0 | 3,0 | ... | 5 | 2 | 6,0 | 2 | 1 | 6,3 | ... |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 32) 15:39 | 5 | 3 | 6,5 | 3 | 0 | 3,0 | ... | 4 | 2 | 5,0 | 1 | 2 | 4,8 | ... |
| 33) 15:44 | 7 | 6 | 10,0 | 5 | 0 | 5,0 | ... | 6 | 3 | 7,5 | 1 | 1 | 7,5 | ... |
| 34) 15:49 | 5 | 4 | 7,0 | 3 | 0 | 3,0 | ... | 4 | 2 | 5,0 | 3 | 2 | 5,3 | ... |
| 35) 15:54 | 5 | 2 | 6,0 | 2 | 0 | 2,0 | ... | 4 | 1 | 4,5 | 3 | 3 | 4,5 | ... |
| 36) 15:59 | 3 | 5 | 5,5 | 1 | 0 | 1,0 | ... | 2 | 2 | 3,0 | 3 | 4 | 2,8 | ... |
| průměr | 5,0 | 2,7 | 6,3 | 3,1 | 0,1 | 3,2 | ... | 4,4 | 1,3 | 5,0 | 2,9 | 2,6 | 5,1 | ... |
Tab. 1 Četnosti chyb typu A a B v původních datech a detekovaných algoritmy ČHMÚ a LASTx i s doplněním o chyby typu C a D (LASTx+) – pro LASTx uvedeno jen LAST4.
V tab. 2 jsou uvedeny úspěšnosti algoritmů ČHMÚ a LAST4 pouze pro chyby typu A a B. Jde o procentuální úspěšnosti přepočtených četností chyb detekovaných algoritmy ČHMÚ a LAST4 ku přepočteným četnostem okem pozorovatelných chyb podle vzorců (5) až (11) pro potřeby hodnocení rozdílu v úspěšnosti detekování jednotlivých druhů chyb (resp. chyb typu A a B). Průměrná procentuální úspěšnost detekce chyby typu A je 64 % pro algoritmus ČHMÚ a 89 % pro algoritmus LAST4. Průměrná procentuální úspěšnost detekce chyby typu B je 4 % pro algoritmus ČHMÚ a 48 % pro algoritmus LAST4. Obr. 6 znázorňuje kompletní data z tab. 2 pro celý algoritmus LASTx.
| parametr → | A | B | ||||||
| čas měření ↓ | PNAč | ... | PNA4 | ... | PNBč | ... | PNB4 | ... |
| 01) 13:04 | 86 % | ... | 86 % | ... | 0 % | ... | 0 % | ... |
| 02) 13:09 | 60 % | ... | 100 % | ... | 0 % | ... | 67 % | ... |
| 03) 13:14 | 29 % | ... | 100 % | ... | 0 % | ... | 100 % | ... |
| 04) 13:19 | 71 % | ... | 100 % | ... | N/A | ... | N/A | ... |
| 05) 13:24 | 60 % | ... | 100 % | ... | 0 % | ... | 67 % | ... |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 32) 15:39 | 60 % | ... | 80 % | ... | 0 % | ... | 67 % | ... |
| 33) 15:44 | 71 % | ... | 86 % | ... | 0 % | ... | 50 % | ... |
| 34) 15:49 | 60 % | ... | 80 % | ... | 0 % | ... | 50 % | ... |
| 35) 15:54 | 40 % | ... | 80 % | ... | 0 % | ... | 50 % | ... |
| 36) 15:59 | 33 % | ... | 67 % | ... | 0 % | ... | 40 % | ... |
| průměr | 64 % | ... | 89 % | ... | 4 % | ... | 48 % | ... |
Tab. 2 Vypočtené úspěšnosti algoritmů ČHMÚ a LASTx pouze pro chyby typu A a B – pro LASTx uvedeno jen LAST4.
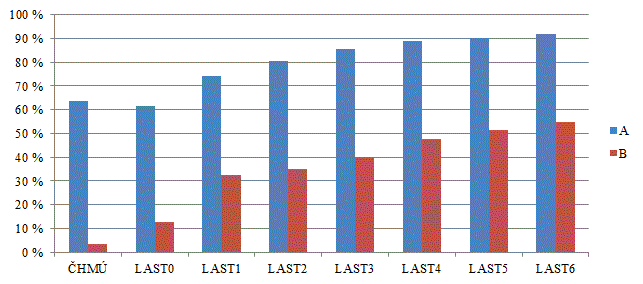
Obr. 6 Vypočtené úspěšnosti algoritmů ČHMÚ a LASTx pouze pro chyby typu A a B.
V tab. 3 jsou uvedeny celkové úspěšnosti algoritmů ČHMÚ a LAST4 vypočítané podle vzorců (7) a (10) a také celková úspěšnost algoritmu LAST4 i se započítáním chyb typu C a D (LAST4+) vypočítaná podle vzorce (11). Průměrná procentuální úspěšnost detekce chyby typu A i B vychází 50 % pro algoritmus ČHMÚ a 80 % pro algoritmus LAST4. Se započítáním chyb typu C a D vychází průměrná procentuální úspěšnost algoritmu LAST4 (LAST4+) 83 %. Obr. 7 znázorňuje kompletní data z tab. 3 pro celý algoritmus LASTx.
| parametr → | AB(+) | ||||
| čas měření ↓ | PNABč | ... | PNAB4 | PNAB4+ | ... |
| 01) 13:04 | 63 % | ... | 63 % | 63 % | ... |
| 02) 13:09 | 46 % | ... | 92 % | 100 % | ... |
| 03) 13:14 | 27 % | ... | 100 % | 100 % | ... |
| 04) 13:19 | 71 % | ... | 100 % | 111 % | ... |
| 05) 13:24 | 46 % | ... | 92 % | 96 % | ... |
| ... | ... | ... | ... | ... | ... |
| 32) 15:39 | 46 % | ... | 77 % | 73 % | ... |
| 33) 15:44 | 50 % | ... | 75 % | 75 % | ... |
| 34) 15:49 | 43 % | ... | 71 % | 75 % | ... |
| 35) 15:54 | 33 % | ... | 75 % | 79 % | ... |
| 36) 15:59 | 18 % | ... | 55 % | 59 % | ... |
| průměr | 50 % | ... | 80 % | 83 % | ... |
Tab. 3 Vypočtená celková úspěšnost algoritmů ČHMÚ a LASTx i se započítáním chyb typu C a D (LASTx+) – pro LASTx uvedeno jen LAST4.
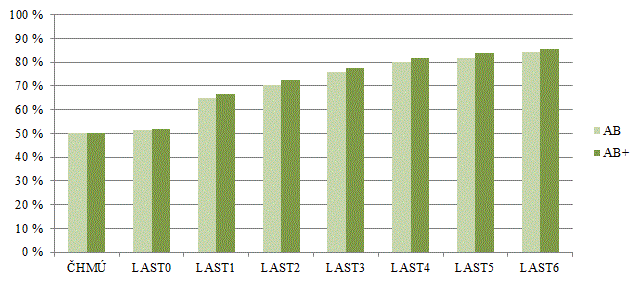
Obr. 7 Vypočtená celková úspěšnost algoritmů ČHMÚ a LASTx i se započítáním chyb typu C a D (LASTx+).
Posledním typem sledovaných chyb je chyba detekovaná algoritmem s negativním dopadem – chyba typu E. Vyhodnocován jen celkový počet na všechny vzorky daného algoritmu. Chyba typu E, jelikož má na výsledek negativní dopad, je nepřístupná a její četnost musí být nulová. Obr. 8 ukazuje, že algoritmy LAST5 a LAST6 vykazují nenulový počet chyb typu E.
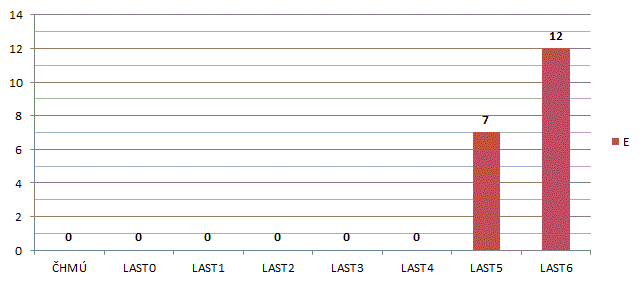
Obr. 8 Chyby detekované algoritmem s negativním dopadem.
Statistické posouzení významnosti rozdílů v hodnocení úspěšnosti algoritmu ČHMÚ a algoritmu LASTxJak jsme uváděli výše, pro statistické posouzení významnosti rozdílů v hodnocení úspěšnosti algoritmu ČHMÚ a algoritmu LASTx jsme stanovili nulovou hypotézu H0: Mezi úspěšností algoritmu ČHMÚ a úspěšností algoritmu LASTx není rozdíl. Alternativní hypotéza zní HA: Úspěšnost algoritmu LASTx je jiná (lepší) než úspěšnost algoritmu ČHMÚ.
V tab. 4 jsou uvedeny zásadní výsledky párového t-testu: rozdíly párových dat, jejich aritmetický průměr, směrodatná odchylka vypočítaná podle vzorce (12) a výsledná hodnota testovací statistiky podle vzorce (13). Sledovali jsme rozdíl četností detekce samostatných chyb typu A a B, tak rozdíl přepočtených četností obou typů chyb A i B, tak s připočtením chyb typu C i D. Rozdíly jsou kalkulovány vždy jako hodnoty algoritmu LASTx umenšené o hodnoty algoritmu ČHMÚ. Pro zvolenou hladinu spolehlivosti 99 %, resp. hladinu významnosti α = 0,01 při stupni volnosti 35 vychází kritická hodnota testového kritéria t0,05(35) = 2,724 [14]. Z tab. 4 je patrno, že pro všechny z přepočtených četností v případě algoritmu LAST4 je vypočítaná hodnota testového kritéria několikrát větší než kritická hodnota t0,05(35), čili odmítáme nulovou hypotézu H0 a přijímáme hypotézu alternativní HA.
| Rozdíl párových dat di |
Aritmetický průměr |
Směrodatná chyba |
Testovací statistika t |
| ... | ... | ... | ... |
| NA4 – NAč | 1,22 | 0,17 | 7,02 |
| NB4 – NBč | 1,25 | 0,18 | 7,13 |
| NAB4 – NABč | 1,85 | 0,20 | 9,28 |
| NAB4+ – NABč | 1,94 | 0,23 | 8,54 |
| ... | ... | ... | ... |
Tab. 4 Výsledné hodnoty párového t-testu.
Kompletní závislost výsledných hodnot testovací statistiky na použitém algoritmu, resp. na počtu x v algoritmu LASTx, je znázorněna na obr. 9. Algoritmy LAST0 a LAST1 vykazují některé ze sledovaných hodnot testového kritéria pod kritickou hodnotou, čili přijímáme nulovou hypotézu H0 a odmítáme hypotézu alternativní HA. Naopak, příznivě pro LASTx, je tomu u LAST2 až LAST6.
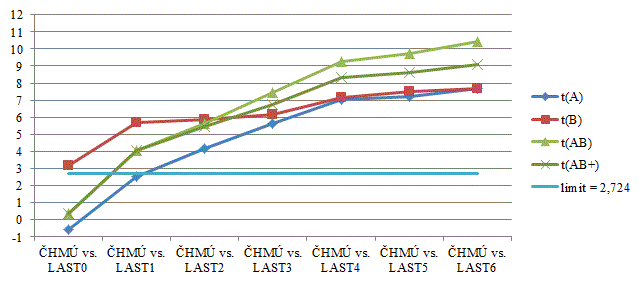
Obr. 9 Výsledné hodnoty testovací statistiky.
Diskuse
Z výsledků je zřejmé, že nově vyvinutý algoritmus LASTx (s výjimkou LAST0) vykazuje pozorovatelně lepší eliminace chyb typu A i B než výsledky algoritmu ČHMÚ. Výsledné snímky jsou tak snáze uchopitelné pro automatické vyhodnocování nebezpečných meteorologických jevů, neboť neobsahují tolik falešných meteorologických cílů, viz obr. 4 a 5.
Z výsledků dále vyplývá, že průměrné hodnoty četností detekce jednotlivých typů chyb a průměrné hodnoty úspěšnosti algoritmu v detekci chyb jsou vyšší pro algoritmus LASTx (u chyby typu A s výjimkou LAST0) než pro algoritmus ČHMÚ – průměrná procentuální úspěšnost detekce chyby typu A i B vychází 50 % pro stávající algoritmus ČHMÚ a 51 % (LAST0) až 84 % (LAST6) pro nový algoritmus LASTx. Se započítáním chyb typu C a D vychází průměrná procentuální úspěšnost algoritmu LASTx 52 % (LAST0) až 85 % (LAST6), viz tab. 2 a 3 a obr 6 a 7. Úspěšnost algoritmu LASTx tedy roste s rostoucím počtem časově předchozích radarových dat x zahrnutých do algoritmu. Zároveň s touto rostoucí úspěšností však roste i počet chyb typu E, detekovaných algoritmem s negativním dopadem, které se vyskytují pro LAST5 a LAST6, což vylučuje jejich použití. Použitelným algoritmem LASTx je z hlediska úspěšnosti LAST0 až LAST4.
Důležité výsledky přineslo i statistické zhodnocení rozdílů úspěšností algoritmů ČHMÚ a LASTx. Z obr. 9 je patrné, že s rostoucí úspěšností souvisí i růst testovací charakteristiky. Algoritmy LAST0 a LAST1 však vykazují některé ze sledovaných hodnot testového kritéria pod kritickou hodnotou, čili přijímáme nulovou hypotézu H0 a odmítáme hypotézu alternativní HA. Použitelným algoritmem LASTx je z hlediska statistiky LAST2 až LAST6.
Celkově tedy výsledky ukázaly, že použitelným algoritmem LASTx je LAST2 až LAST4, přičemž LAST4 dosahuje nejlepších výsledků úspěšnosti (80 %) oproti úspěšnosti původního algoritmu ČHMÚ (50 %).
Závěr
V tomto článku jsme představili nový algoritmus detekce a eliminace negativního vlivu radioreléových spojů na meteorologická radarová měření založený na aplikaci metod zpracování obrazu s využitím informací ze zpracování časově předchozích radarových dat (pracovní název nového algoritmu je LASTx). Cílem tohoto článku bylo porovnat výsledky vyvinutého algoritmu LASTx s výsledky stávajícího, v ČR operativně používaného algoritmu ČHMÚ a navrhnout optimální počet časově předchozích radarových dat x zahrnutých do algoritmu. Porovnání na sadě 36 radarových snímků prokázalo, že námi vyvinutý algoritmus LASTx dosahuje statisticky významně lepších výsledků při detekci a eliminaci rušení radioreléových spojů z meteorologických radiolokačních měření. Zlepšena je zejména detekce a eliminace slabšího rušení projevujícího se přerušovanými liniemi. Jako optimální počet časově předchozích radarových dat x zahrnutých do algoritmu LASTx se ukázalo 2 až 4, z toho LAST4 dosahuje nejlepších výsledků úspěšnosti. Velmi nadějné výsledky metody LASTx získané na testovaném vzorku dat vedly k rozhodnutí implementovat metodu LASTx do operativního zpracovatelského software ČHMÚ, kde bude moci být v paralelním experimentálním běhu testována v reálném čase na operativních aktuálně měřených datech. Tento paralelní běh umožní důkladnější testování metody LASTx na větším množství dat s různým typem meteorologických odrazů i rozmanitější intenzitou a prostorovým rozložením rušení. Po úspěšném otestování v tomto paralelním běhu bude moci být metoda LASTx nasazena do operativního zpracování radarových dat v ČHMÚ.
Rádi bychom poděkovali Českému hydrometeorologickému ústavu za poskytnutá radarová data pro náš výzkum.
Literatura
[1] CHMELA, L. Automatická analýza meteorologické situace. Praha, 2008. 85 s. ČVUT v Praze. Vedoucí diplomové práce Ing. Jaroslav Burčík, Ph.D.
[2] CHMELA, L.; BURČÍK, J. Meteorological Image Processing in Automated Systems. In Proceedings of IWSSIP 2008. 15th International Conference on Systems, Signals and Image Processing. Bratislava: Slovak University of Technology in Bratislava, 2008, p. 527–530. ISBN 978-80-227-2856-0.
[3] CHMELA, L.; BURČÍK, J. Negativní vliv radioreléových spojů na meteorologická radarová měření. In Sborník příspěvků konference KRÁLÍKY 2009. Brno: VUT v Brně, FEKT, 2009, s. 109–112. ISBN 978-80-214-3938-2.
[4] ŽEJDLÍK, T.; NOVÁK, P. Frequency Protection of the Czech Weather Radar Network. In ERAD 2010 - The Sixth European Conference on Radar in Meteorology and Hydrology. Sibiu, 06.–10.09.2010.
[5] CHMELA, L.; BURČÍK, J. Detection of Negative Impact of Radio Relay Communication on the Weather Radar Measurement by Using Hough Transform. In Knowledge in Telecommunication Technologies and Optics 2010 - KTTO 2010. Ostrava: VSB-Technical University of Ostrava, 2010, s. 153–157. ISBN 978-80-248-2330-0.
[6] CHMELA, L.; BURČÍK, J. Vliv použitého algoritmu detekce hran: Identifikování negativního vlivu radioreléových spojů na meteorologická radarová měření s využitím Houghovy transformace. In Modernizace vysokoškolské výuky technických předmětů [CD-ROM]. Hradec Králové: Gaudeamus, 2011, s. 50–53. ISBN 978-80-7435-110-5. ISSN 1214-0554.
[7] NOVÁK, P. – HAVRÁNEK, P. - KRÁČMAR J. Česká meteorologická radarová síť CZRAD v roce 2008. In Meteorologické Zprávy, 61, 2008, 129-136.
[8] NOVÁK, P. Definice formátu radarových dat ČHMÚ-OR. verze 1.2 (28. 6. 2006). Praha: ČHMÚ, 2006.
[9] IEEE Std 686™-2008: IEEE Standard Radar Definitions. New York: IEEE Aerospace and Electronic Systems Society: 2008.
[10] QIDWAI, U. – CHEN, C.H. Digital Image Processing: An Algorithmic Approach with MATLAB. Boca Raton: Chapman & Hall/CRC, 2010. ISBN 978-1-4200-7950-0.
[11] GONZALEZ, R.C. - WOODS, R.E. Digital Image Processing. New Jersey: Pearson Education, Inc., 2008. ISBN 978-0-13-168728-8.
[12] SONKA, M. – HLAVAC, V. - BOYLE, R. Image Processing, Analysis and Machine Vision. Toronto: Thomson, 2008. ISBN 978-0-459-08252-1.
[13] HENDL, J. Přehled statistických metod zpracování dat: Analýza a metaanalýza dat. Praha: Portál, 2004. ISBN 80-7178-820-1.
[14] CHRÁSKA, M. Metody pedagogického výzkumu: Základy kvantitativního výzkumu. Praha: Grada, 2007. ISBN 978-80-247-1369-4.
[15] MELOUN, M. – MILITKÝ, J. Statistická analýza experimentálních dat. Praha: Academia, 2004. ISBN 80-200-1254-0.