Pokročilé modelování přeslechu na vzdáleném konci – generování průběhů

Příspěvek představuje výsledky statistického zpracování parametrů modelu přeslechu FEXT pro jednotlivé konstrukční skupiny kabelu a jeho následné doplnění o generování pseudonáhodných frekvenčních průběhů.

---

Advanced crosstalk modelling - generating of characteristics

Abstract

The paper follows previous publication, gives new insights in FEXT simulation based on metallic cable constructional arrangement using statistical evaluation of measured parameters. This statistical model is subsequently modified by generated random waveform to simulate realistic results using statistical values of measured characteristic and its filtration.

---

Úvod

V předchozím článku Pokročilé modelování přeslechu – měření a předpoklady představená idea generátoru přenosových funkcí přeslechů nabízí podstatné zjednodušení výpočtů a simulací přeslechu FEXT díky jeho rozložení na příspěvky jednotlivých konstrukčních kategorií kabelu. V případě doplnění modelu náhodně generovanou složkou frekvenční závislosti, odvozenou statistickým zpracováním naměřených hodnot a její následnou filtrací, je možné získat pokročilý statistický model útlumu přeslechu FEXT, který následně napodobuje parametry skutečných kabelů bez nutnosti časově náročných měření.

Standardní model přeslechu FEXT

Zjednodušený model přeslechu FEXT vychází z odvození kapacitních a induktivních vazeb, blíže se této problematice věnuje [1]. Přenosová funkce výkonu přeslechu FEXT lze pak vyjádřit:

(1)

Kde

|HFEXT(f)|2	představuje přenosovou funkci výkonu přeslechu
|H(f)|2	je přenosová funkce výkonu vedení
KFEXT	je parametr (konstanta pro daný pár) závislý na typu kabelu a vzdálenosti uvažovaných párů

Přenosová funkce výkonu symetrického páru lze vyjádřit pomocí sekundárního parametru vedení α(f), více viz [2]. Pro určení parametru α(f) byla použita aproximace pomocí modelu British Telecom (BT), prezentovaném např. v [3]. Model útlumu přeslechu FEXT se nejčastěji zobrazuje po logaritmování vztahu (1) v dB, což bude použito i dále.

Charakter přeslechu ve vztahu (1) určuje parametr K_FEXT. Ten závisí jednak na použitém materiálu kabelu, jeho výrobě a uložení, ale rovněž na pozici uvažovaného rušeného a rušícího páru v něm a při aproximaci všech naměřených hodnot v kabelu je obecně pro každou kombinaci párů individuální. Díky předchozím předpokladům o geometrickém uspořádání kabelu lze získané závěry zohlednit i pro určení tohoto parametru. Parametr K_FEXT lze použít pro odhad přeslechu z jednoho rušícího párů, ale zejména pro výpočet rušení z více rušících zdrojů (párů). Z toho vyplývá, že je nutný přepočet (rozšíření modelu) pro různé počty rušících přípojek. V příspěvku [2] je prezentována dvojice modelů: model mocninný, který představuje přidávání rušících systémů do kabelu počínaje od nejhoršího možného případu, druhým modelem je lineární model s vyjádřením přepočtu pro n zdrojů rušení

(2)

který vychází z lineárního nárůstu rušení, kdy jsou rovnoměrně obsazovány pozice rušícími systémy. Pro další výpočty a úvahy byl zvolen právě tento model (2).

Pro ověření změřených výsledků a modelu útlumu přeslechu FEXT dle předchozích vzorců (1, 2) byl vybrán rušený pár číslo 1. Výpočtem byl stanoven sumární útlum přeslechu FEXT a jeho model, výsledek znázorňuje obr. 1.

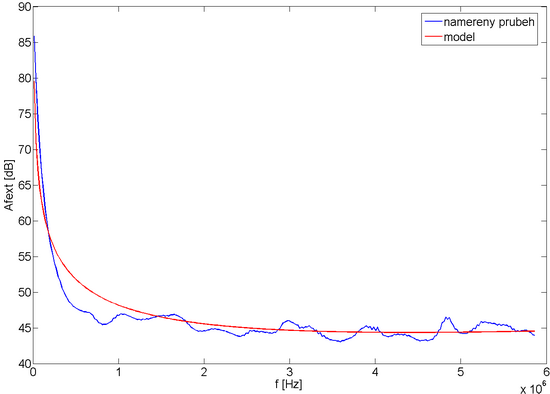Obr. 1: Porovnání sumárního útlumu přeslechu FEXT a modelu útlumu přeslechu FEXT pro pár číslo 1.

Z porovnání je zřejmé, že se model útlumu přeslechu A_FEXT v pásmu do 6 MHz blíží změřeným hodnotám. Další vyhodnocení bylo provedeno s ohledem na odlišení příspěvků od jednotlivých podskupin pro potvrzení úvah vycházejících z geometrické konstrukce kabelu. Pro ilustraci byl opět vybrán pár číslo 1, výsledek je znázorněn na obr. 2, který potvrzuje dominantní vliv přeslechů od párů ve stejné podskupině.

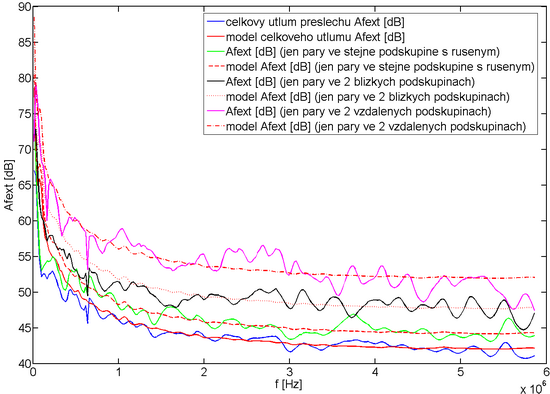Obr. 2: Rozdělení útlumu přeslechu FEXT na příspěvky jednotlivých podskupin a jejich modely.

Pokročilý model přeslechu FEXT

Základní ideou pokročilého modelování přeslechu FEXT je stanovení různých hodnot přeslechového parametru K_FEXT podle konstrukčního uspořádání kabelu. Zatímco při standardním přístupu je uvažována jediná hodnota (průměrná nebo nejhorší možná podle použitého modelu) pro celý kabel, umožňuje pokročilý model zohlednit vztah rušeného a rušícího páru na základě jejich pozic v kabelu. Přináší tak výrazné zvýšení přesnosti modelu při zachování dostatečně nízkého počtu parametrů oproti individuálnímu modelování všech kombinací párů v kabelu. Nejprve je však nutné určit hodnoty parametru K_FEXT pro jednotlivé podskupiny v kabelu.

Prvním krokem je vytvoření matice, která obsahuje ve sloupcích jednotlivé rušené páry (50 sloupců), na řádcích pak rušící páry (49 řádků), v průsečíku sloupce i a řádku k se tak nachází parametr K_FEXT pro rušený pár i a rušící pár k. Páry jsou zde umístěny vždy tak, aby odpovídaly geometrickému uspořádání kabelu, jednotlivé podskupiny jsou přemístěny stejně jako v případě předchozí analýzy zdrojů rušení. Následně je pro každou konstrukční kategorii určena střední hodnota a rozptyl normálního rozložení parametru K_FEXT, výsledkem je tak určení 3 středních hodnot a 3 hodnot rozptylu pro celý kabel. Porovnání rozdílu mezi individuálním určením parametru K_FEXT a použitím statistické hodnoty znázorňuje obr. 3.

Obr. 3: Porovnání naměřené hodnoty, standardního modelu a statistického modelu útlumu přeslechu FEXT pro kombinaci párů číslo 1 a 42.

Z porovnání obou modelů je zřejmé, že se statistický model přesností blíží standardnímu, který byl určen individuálním výpočtem pro zvolenou kombinaci rušeného a rušícího páru. Přitom pro vygenerování statistického modelu libovolné kombinace dvou párů je potřeba jen 3 středních hodnot a 3 hodnot rozptylu pro celý kabel, což přináší nemalé zjednodušení celého procesu a snížení potřebné výpočetní náročnosti.

Nevýhodou modelu vzniklého proložením poměrně jednoduché funkce (1) oproti naměřeným hodnotám je absence charakteristického rozvlnění frekvenčního průběhu s dosti značným rozkmitem. Pro splnění požadavku na co nejreálnější generování přeslechových charakteristik je proto potřeba statistický model vhodně doplnit o pseudonáhodnou složku.

Pro každou kombinaci rušeného a rušícího páru je nejprve vytvořena rozdílová funkce pro kombinaci párů i, k pro každý bod frekvenční charakteristiky. Na základě předchozích závěrů ohledně geometrického uspořádání kabelu jsou z hodnot rozdílové funkce pro jednotlivé konstrukční kategorie párů určeny rozptyly rozvlnění normálního rozložení přes celé uvažované frekvenční pásmo. Pomocí těchto hodnot lze náhodně vygenerovat pro zvolenou kombinaci párů i, k pseudonáhodnou rozvlňující charakteristiku a přidat ji k hodnotě modelu.

(3)

Ve vzorci (3) představuje FEXT_Gen(f)_i,k statistický model FEXT_Mod(f)_i,k s přidanou vygenerovanou rozvlňující složkou FEXT_Rnd(f)_i,k. Předchozí výpočty a simulace byly z důvodu přílišného rozdílu mezi naměřenými hodnotami a modelem omezeny pro frekvenční pásmo do zhruba 6 MHz (viz závěry v předchozím článku), model BT, náhodné rozvlnění a výsledný model je však opět generován pro celé uvažované frekvenční pásmo do 34 MHz s použitím statistických parametrů určených pro pásmo do 6 MHz. Výsledek je prezentovaný na následujícím obr. 4.

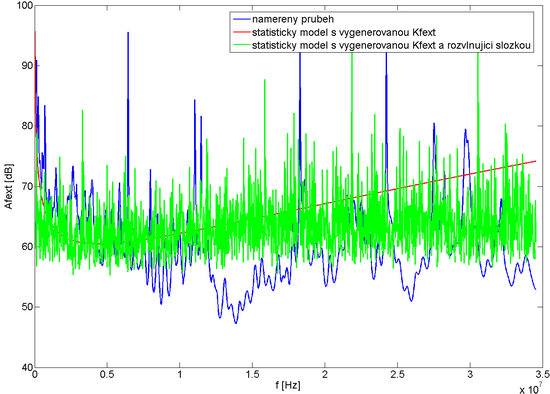Obr. 4: Výsledek přidání náhodné složky ke statistickému modelu útlumu přeslechu FEXT pro kombinaci párů číslo 1 a 33 a frekvenční pásmo do 34 MHz.

Na první pohled je však patrné, že díky náhodně generované složce na každém frekvenčním kroku, je výsledkem charakteristika neodpovídající reálné situaci. Porovnáním spekter obou závislostí díky provedené Fourierově transformaci bylo navrženo provedení filtrace průběhů s náhodnou složkou a také odvozeny potřebné parametry filtrů. Celý proces filtrace byl pro zjednodušení a použití filtrů nižších řádů rozdělen do 3 kroků. V prvním byla odstraněna stejnosměrná složka a potlačeny složky na počátku spektra použitím strmého IIR filtru typu horní propust odvozeného z analogového filtru s Butterworthovou charakteristikou. Následným IIR filtrem typu pásmová zádrž byl potlačen vliv složek ve střední části spektra (filtr byl opět odvozen z analogového filtru s Butterworthovou charakteristikou). V poslední fázi byly odstraněny drobné překmity a nerovnoměrnosti FIR vyhlazovacím filtrem. Došlo tak k drobné úpravě schématu generátoru přenosových funkcí přeslechů prezentovaném v předešlém článku, kdy se filtrace místo původně plánované jen pro rozvlňující složku provádí až po jejím součtu se statistickým modelem. Následující obr. 5 představuje výsledný průběh pro filtraci, který se již svým charakterem značně přibližuje skutečným frekvenčním charakteristikám přeslechu.

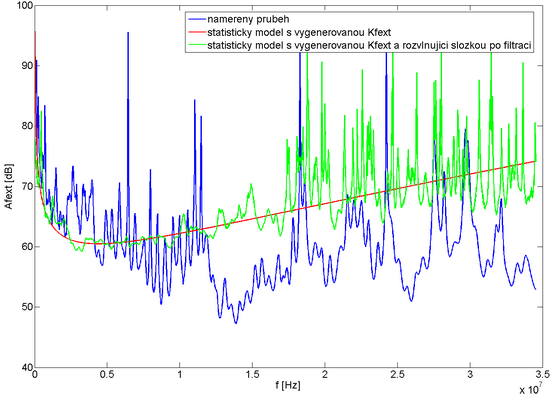Obr. 5: Předchozí statistický model útlumu přeslechu FEXT s přidanou rozvlňující složkou po provedené filtraci pro kombinaci párů číslo 1 a 33 a frekvenční pásmo do 34 MHz.

Závěr

Výše uvedené možnosti modelování přeslechu na základě geometrické konstrukce kabelu mohou podstatně snížit náročnost jeho výpočtu a simulace. Díky rozdělení a analyzování přeslechu dle podskupin v kabelu lze určit podíl jednotlivých konstrukčních kategorií a jejich vliv na celkový přeslech. Na základě statistického zpracování je možné vyjádřit hodnoty přeslechového parametru K_FEXT pro jednotlivé podskupiny, tj. 3 střední hodnoty a 3 hodnoty rozptylu normálního rozložení.

Pro vytvoření modelu dostatečně věrně simulujícímu reálné průběhy útlumu přeslechu FEXT v závislosti na frekvenci je potřeba statistický model doplnit pseudonáhodnou složkou, jejíž parametry byly rovněž odvozeny statistickými metodami. Po filtraci výsledného průběhu tak lze popsaný postup použít pro generování individuálních pseudonáhodných přenosových funkcí přeslechu na vzdáleném konci pro modelování přenosového prostředí přípojek xDSL s modulací VDMT a ověření její schopnosti potlačovat přeslechy za nejrůznějších podmínek bez nutnosti časově náročných měření.

Tento článek vznikl za podpory výzkumného záměru MSM6840770014.

Literatura

[1] Rauschmayer, Dennis J.: ADSL/VDSL Principles: A Practical and Precise Study of Asymmetric Digital Subscriber Lines and Very High Speed Digital Subscriber Lines. Macmillan Technical Publishing, Indianapolis, USA, Nov. 1998. ISBN 1-57870-015-9.
[2] Vodrážka, J.: Modely pro symetrické páry v místních kabelech. Elektrorevue [online]. 2004, roč. 5, č. 2004/56, s. 2004/56. [cit. 2008-9-1]. Internet: http://www.elektrorevue.cz/clanky/04056/. ISSN 1213-1539 [cit. 2008-11-07].
[3] Vodrážka, J.: Modelování metalických účastnických přípojek. Access server [online], Internet: http://access.fel.cvut.cz/view.php?cisloclanku=2001012601. 2004, roč. 2. ISSN 1214-9675. [cit. 2008-11-07].