Optimalizace nehierarchické telekomunikační sítě

Článek definuje problém optimalizace nehierarchické telekomunikační sítě a rozebírá složitost tohoto problému.

(Text článku ve formátu pdf je k dispozici na adrese http://k332.feld.cvut.cz/hudousek/data/access-optim/optim.pdf.)

Úvod

Při plánování rozšíření či výstavby nové telekomunikační sítě hrají důležitou roli postupy, které vedou z ekonomického hlediska k optimálnímu řešení. Vedle problémů čistě ekonomických, jako je nalezení zdrojů pro financování operace, atp. je nutné řešit i problémy, které přímo souvisejí s technickou realizací sítě samotné - je nutné odpovídajícím způsobem navrhnout uspořádání a počty prvků v síti. Tato činnost obvykle vychází z příslušných matematických modelů sítě a provozního zatížení v ní odbavovaného. Cílem této práce je zformulovat zobecněný problém optimálního návrhu sítě, shrnout jeho vlastnosti a navrhnout možné typy algoritmů, které by byly použitelné pro jeho řešení.

Formulace problému

Je dán souvislý, jednoduchý, neorientovaný graf G = (V, E), kde V={v₁, v₂, ..., v_N} je množina vrcholů a E={e₁, e₂, ..., e_M} množina hran reprezentujících potenciální svazky mezi uzly sítě. Dále je dána matice nabízeného provozního zatížení A, kde každý z prvků a_i,j je uspořádanou n-ticí parametrů popisujících provozní zatížení mezi dvojicí uzlů i a j. Pro každou hranu e_k je také dána ohodnocující funkce C_k(A_k, D_k), kde a_k je uspořádaná n-tice parametrů popisujících provozní zatížení nabízené svazku, který je reprezentován hranou e_k. Uspořádaná n-tice parametrů D_k pak popisuje omezující podmínky nutné pro výpočet ohodnocující funkce, např. maximální přípustnou ztrátu svazku. Cílem úlohy je nalézt cesty P_i,j mezi všemi dvojicemi uzlů i, j, mezi nimiž existuje nenulová nabídka, takové, aby byla minimalizována kriteriální funkce¹

(1)

Provozní zatížení A_i,j přispívá k provoznímu zatížení, které je nabízeno hraně e_k, zatížením a_(i,j)(k)>= 0. Hodnota kriteriální funkce bude v dalším textu označována též jako celková cena. Např. v případě modelování hran sítě jako systémů M/M/N/0 Kendallovy klasifikace a za předpokladu směrování bez přelivu jsou prvky matice nabízeného provozního zatížení A střední hodnoty nabízeného provozního zatížení a_i,j. K-té hraně na cestě mezi uzly i a j je nabízeno provozní zatížení

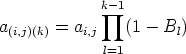(2)

a parametrem a_k popisujícím provozní zatížení nabízené hraně e_k je pak, za předpokladu nezávislosti jednotlivých nabízených toků provozního zatížení, hodnota

(3)

Pro dimenzování svazku odpovídajícího hraně k lze pak použít dobře známý 1.Erlangův vztah E_1,NO(A) pro výpočet ztráty systému M/M/N/0.

Předpokládáme-li lineární závislost ceny na počtu okruhů N_O² tvořících svazek a předepsanou ztrátu svazku B_pr je celková cena C_k dána rovnicemi:

Počet řešení problému³

Počet možných řešení problému závisí na počtu a uspořádání hran, proto budou vymezeny pouze krajní případy. Nejmenší počet řešení existuje, pokud je graf kostrou, tj. pokud je stromem a obsahuje tolik hran, že odebráním kterékoliv z nich by přestal být souvislý. V takovém případě existuje mezi každou dvojicí uzlů právě jedna cesta a úloha má tedy jediné řešení. Největší počet řešení existuje, pokud je graf úplný. Pak graf mezi dvojicí uzlů obsahuje NC_l cest délky l:

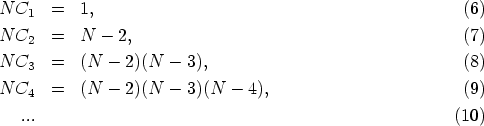
Počet různých cest délky k mezi dvojicí uzlů je tedy

(11)

kde N je počet uzlů grafu. Maximální délka cesty mezi dvěma uzly je N-1 a celkový počet různých cest mezi dvojicí uzlů je tedy

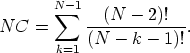(12)

V grafu o N uzlech je N(N-1)/2 různých dvojic uzlů, předpokládá se, že cesty P_i,j a P_j,i jsou až na opačné pořadí prvků totožné a celkový počet možných kombinací cest mezi všemi dvojicemi uzlů je:

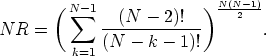(13)

Rychlý růst počtu řešení problému s rostoucím počtem uzlů grafu je ilustrován v následující tabulce:

N	NC	NR
31 41 51 61 71 81 91 101 151 201	21 51 161 651 3261 19571 137001 1096011 1,69.1010 1,74.1016	81 156251 1,09.1012 1,56.1027 5,99.1052 1,46.1092 8,36.10148 6,19.10226 1,00.101074 5,26.103085

Složitost problému⁴

Složitost problému je posuzována podle složitosti algoritmu, který daný problém řeší. Složitost algoritmu je rozlišována dvojího druhu:

• časová podle času potřebného k provedení algoritmu,
• paměťová podle velikosti paměti potřebné pro provedení algoritmu.

Časová složitost problémů

Absolutní čas vykonávání konkrétního programu závisí na celé řadě okolností, které jsou často obtížně reprodukovatelné a pro řešení vlastního problému nepodstatné. Proto se místo toho sleduje pouze závislost počtu elementárních operací, resp. času potřebného k jejich vykonání na rozsáhlosti zadání úlohy. Význam elementární operace se však liší podle konkrétního algoritmu, v některých případech se započítávají všechny operace, které musely být v průběhu algroritmu vykonány. Častěji se však sledují pouze ty, jejichž vliv na celkovou dobu vykonávání algoritmu je největší, např. násobení a dělení. Interpretace pojmu velikost zadání úlohy taktéž záleží na konkrétním typu úlohy. Například pro algoritmy zpracovávající text jí může být počet znaků textu, pro úlohy, které pracují s grafy, může být za velikost úlohy považován, jak je tomu i v případě této práce, počet uzlů vstupního grafu. Počet operací, které musejí být vykonány, závisí na zadání úlohy. Určitým řešením tohoto problému by bylo sledovat průměrnou složitost algoritmu. Obecně by pak ovšem muselo být známé rozložení pravděpodobnosti výskytu konkrétních zadání úlohy, a proto se často dává přednost analýze krajních případu, minimální a zejména maximální složitosti.

Aby se problém dále zjednodušil srovnává se složitost algoritmů (funkce velikosti zadání úlohy) až na multiplikativní konstantu. Složitost algoritmu se pak označuje O(f(n)). kde f(n) je libovolná funkce velikosti zadání n, a platí, že doba T(n) potřebná pro vykonání algoritmu pro vstup velikosti n je T(n) < kf(n) pro nějakou konstantu k a od nějakého n₀, tj. pro n>n₀. Za prakticky použitelné (zvládnutelné, angl. tractable) se považují takové algoritmy, kde f(n) je polynom. Naproti tomu algoritmy, pro které je f(n) exponenciální funkce nebo rychleji rostoucí funkce se pokládají za nezvládnutelné. V praxi samozřejmě záleží na stupni daného polynomu a multiplikativní konstantě. Doba potřebná pro vykonání algoritmu se složitosti O(n¹⁰⁰) může být pro prakticky se vyskytující velikosti zadání úlohy značně větší než pro algoritmus se složitostí O(2ⁿ), ačkoliv první m8 slo6itost polynomiální a druhý exponenciální. Ve většině případů však naznačené dělení platí.

Uvedená úloha, tak jak byla v úvodu práce zformulována, je úlohou optimalizační. Cílem je nalézt nejlepší řešení, tj. zde takové, jehož celková cena f je minimální. V teorii složitosti se pracuje často s tzv. rozhodovacími úlohami, tj. takovými úlohami, jejichž řešením je buď odpověď ANO nebo odpověď NE (viz [4]). Ke každé optimalizační úloze lze sestrojit její odpovídající rozhodovací verzi. Její součástí je oproti optimalizační verzi navíc číslo K a cílem je rozhodnout, zda existuje řešení, jehož cena (hodnota kriteriální funkce f) je menší nebo stejná jako K (K > f). Je zřejmé, že nalezení řešení optimalizační verze úlohy je nejméně tak složité jako nalezení řešení její rozhodovací verze. Na druhou stranu lze dokázat, že pokud existuje algoritmus s polynomiální složitostí, který řeší danou rozhodovací verzi úlohy, pak je polynomiálně řešitelná i její optimalizační verze [5].

Úlohy se v teorii složitosti dělí do tzv. tříd podle toho, jakou složitost má nejlepší algoritmus pro jejich řešení. Třída P je třída všech rozhodovacích úloh, pro které existuje algoritmus se složitostí O(p(n)) pro nějaký polynom p(n). Další významnou třídou je NP, do níž patří všechny rozhodovací úlohy, pro které existuje nedeterministický algoritmus pracující v polynomiálním čase. Rozhodovací úloha patří tedy do NP, pokud v případě, že se podaří odhadnout nějakým způsobem řešení odpovídající optimalizační úlohy, jsme schopni v polynomiálním čase ověřit, zde je řešením rozhodovací úlohy ANO nebo NE. Všechny úlohy z P jsou i v NP, opačný vztah nebyl prokázán a má se za to, že platí P < > NP. NP úloha navíc patří do třídy NP-úplných úloh (ve zkratce NPC), pokud je na ní možné převést každou NP-úlohu algoritmem se složitostí nejvýše O(p(n)). Tj, pokud by se podařilo nalézt polynomiální algoritmus pro libovolnou NP-úplnou úlohu, pak by bylo možné řešit s polynomiální složitostí všechny NP úlohy. Uvedený popis rozdělení do tříd je jen velmi hrubým přiblížením, formálně přesné definice a příslušný výklad lze nalézt například v [5].

Speciálním případem optimalizační úlohy definované na začátku této práce je tzv. problém návrhu sítě (Network Design Problem - NDP), pro který platí, že ohodnocující funkce C_k(A_k,D_k) je lineární. Bylo prokázáno [3], že NDP patří do třídy NP-úplných problémů.

Paměťová složitost problému

Paměťová náročnost daného algoritmu závisí na vhodně zvolené reprezentaci dat. Pro danou úlohu je z hlediska paměťové náročnosti klíčová reprezentace potenciálních řešení úlohy, tj. cest pro všechny dvojice uzlů mezi nimiž existuje nabídka. V dalším textu předpokládejme, že pro uložení jednoho uzlu či hrany je potřeba jednotkové místo v paměti. Variantou nejméně náročnou na prostor je ukládání cesty buď jako posloupnosti uzlů nebo jako posloupnosti hran, potom pro reprezentaci jednoho řešení v nejhorším případě stačí

(14)

míst pro reprezentaci seznamy uzlů (pokud by byly ukládány i oba krajní uzly), resp.

(15)

pro reprezentaci seznamy hran, v obou případech by tedy paměťová složitost byla O(N³). Ve většině algoritmů je zapotřebí mít možnost prohledávat sousední řešení (neighbour solutions), tj. řešení, která se od daného řešení liší jen málo. Pokud je graf G úplný, dají se poměrně jednoduše zkonstruovat algoritmy, které hledají podobná řešení k řešením, kde jsou cesty reprezentovány seznamy uzlů či hran. V takovém případě jsou, při uzlové reprezentaci, pro každou délku l přípustné (až na počáteční a koncový uzel) všechny permutace bez opakování libovolných l-1 uzlů ze zbývajících uzlů. Čím více je ovšem graf neúplný, tím problematičtější může být nalezení nejpodobnějšího přípustného řešení.

V takovém případě se může jevit jako výhodnější předem vytvořit pro každou dvojici uzlů seznam cest (v podobě, jaká byla naznačena výše), které mezi nimi existují. Řešení jsou pak reprezentována pouze odkazy do tohoto seznamu. K reprezentaci samotného řešení je pak sice zapotřebí pouze N(N-1)/2 míst v paměti, avšak seznam cest si může vyžádat i značné množství paměti. Pro všechny cesty délky l mezi dvojicí uzlů je při reprezentaci cesty seznamem uzlů zapotřebí

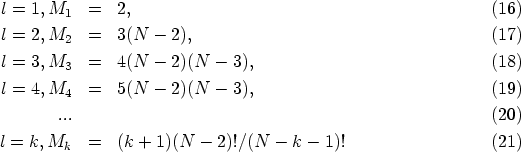
míst v paměti. V nejhorším případě si tak reprezentace všech přípustných cest v grafu může vyžádat

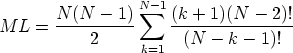(22)

míst v paměti. Pro reprezentaci R řešení je pak zapotřebí R^. N + ML paměťových míst. Maximální nároky na paměť obou přístupů při reprezentování jednoho řešení (R = 1) jsou ilustrovány v následující tabulce:

N	MV	ML+R.N
51 101 151 201 501	401 4051 14701 36101 600251	650+51 44388450+101 2,48.1013+15 6,28.1019+20 1,28.1022+50

Je evidentní, že druhý uvedený přístup je pro zadání o více než deseti uzlech nepoužitelný. Přesto je však výhodný a používaný pro testování různých optimalizačních algoritmů, neboť se jeho použitím značně zjednoduší problém hledání sousedního řešení v neúplných grafech. Pokud by ovšem bylo cílem vytvořit reálnou aplikaci, pak by bylo nutné použít úspornější reprezentaci. Tato práce se ovšem soustředí jen na prozkoumání možných optimalizačních algoritmů, a tak může být využita i paměťově náročná varianta reprezentace.

Příspěvek vznikl za podpory grantu FRVŠ č.2047/2004.

Reference

[1] Hudousek,O. Evaluation of the Erlang-B formula. RTT 2003 - Proceedings. Bratislava: FEI, Slovak University of Technology, 2003, p.80-83.

[2] Hudousek,O. Precision of the Erlang-B Function Evaluation for noninteger number of service lines. Sborník konference RTT 2004. Praha: FEL, České vysoké učení technické, 2004

[3] Johnson.D.S.; Lenstra.J.K.; Rinnooy Kan.A.H.G. The Complexity of the Network Design Problem. Networks, Vol.8 New York: John Wiley & Sons, Inc., 1978, p.279-285

[4] Mařík.V.; Štěpánková.O.; Lažanský.J. a kol. Umělá inteligence (3). Praha: Academia 2001. 328 s. ISBN 80-200-0472-6.

[5] Papadimitrou.C.H. Computational Complexity. Adison-Wesley Publishing Company 1994. 523 s. ISBN 0-201-53082-1.

[6] Pioro.M. et al. Topological design of telecommunication networks (Nodes and links localization under demand constraints). Teletraffic Engineering in the Internet Era: Proceedings of the International Teletraffic Congress - ITC-17 Salvador Da Bahia, Brasilia: Elsevier Science, 2001, p.629-642. ISBN 0444509119.

[7] Rapp, Yngve. Planning of Junction Network in a Multi-exchange Area. I General Principles. Ericsson Technics, 1964, no.1, p.77-130.

[8] Rapp, Yngve. Planning of Junction Network in a Multi-exchange Area. II Extensions of the Principles and Applications. Ericsson Technics, 1965, no.2, p.187-240.

[9] Vidal.V.V.R. et al. Applied Simulated Anealing. Berlin: Springer-Verlag 1993.

---

¹Pro hodnotu kriteriální funkce bude v této práci používáno též označení celková cena.

²V této části je počet okruhů značen N_O místo obvyklého N proto, aby se předešlo záměně s frekventovanějším označením počtu uzlů grafu N.

³Zde se nabízí otázka, zda za řešení problému považovat všechny varianty cest mezi dvojicemi uzlů, mezi nimiž je nenulová nabídka provozního zatížení, nebo jestli za něj považovat pouze tu variantu, pro kterou platí, že kriteriální funkce f je minimální. V dalším textu je použita první variantě a za řešení problému je považována jakákoliv přípustná variantu cest mezi dvojicemi uzlů. Nejlepší z variant je označována jako optimální řešení. Jak je patrné z dalšího, takové řešení lze nalézt pouze ve speciálních případech, jinak je nutné spokojit se s nějakým téměř optimálním řešením.

⁴V následujících odstavcích je mj. uveden velmi stručný přehled teorie složitosti. Bližší informace je možné získat v přehledové podobě v [4], podrobnější výklad problematiky je obsažen např. v [5].