On Robust Control of Adaptive Algorithms for Acoustic Echo Cancellers
Autor: K. Sakhnov, B. Šimák <sakhnk1(at)fel.cvut.cz>, Pracoviště: České vysoké učení technické v Praze, FEL, Téma: Digitální zpracování signálu, Vydáno dne: 31. 12. 20081. Introduction
DT is a major issue present in acoustic echo cancellation (AEC). It occurs when both the far-end and the near-end speakers speak simultaneously. Many attempts have been made to alleviate the isruptive effects of DT; these include the use of DT detection schemes, robust daptive AEC, step-size control, state-space representation ([1], [2]). The scheme f extending robust algorithms to an acoustic hands-free environment as proposed in [3] became the motivation for this paper.
Robust adaptive echo cancellation in particular, is an interesting approach
because if appropriately combined with a good double-talk detector (DTD) it
could offer a noteworthy solution in overcoming the problems of DT [2]. This
approach was used for line echo cancellers (LEC) [3]. Thus, by extending the
method to acoustic hands-free scenarios, it may prove very valuable in the
long term goal of eliminating the problems caused by DT.
As shown in ([4], [5]), faster convergence can be achieved by using
algorithms like Proportional Normalized Least Mean Squares (PNLMS) and
PNLMS++. For LEC, it is reasonable to assume that the echo path is sparse
(i.e. many coefficients are zero), and try to identify only the non-zero
active coefficients. This is the idea behind the PNLMS algorithm which is a
modification of the NLMS. Thus, higher convergence rate is achieved by using
the fact that the active part of network echo path is usually much smaller
(4-8 ms) compared to 64-128 ms of the whole echo path that has to be
covered. In PNLMS, an adaptive individual step-size is assigned to each
filter coefficient.
However, this algorithm does not utilize the fact that the speech signal is
a correlated signal. If this is taken into account, further increase in
convergence rate can be achieved; this thought leads to the Affine
Projection Algorithm (APA) ([6], [7]).
Besides the convergence rate, an important aspect of an echo canceller (EC)
is its performance during DT. To inhibit the divergence of the EC the
standard procedure is to use a level based DTD [8]. Whenever DT is detected
the step-size of the adaptive filtering algorithm is set to zero thus
inhibiting the adaptation. Unfortunately, during the time required by the
DTD to detect DT, the EC often diverges. This is because even a few
undetected amplitude samples perturb the echo path estimate considerably
[3]. Once this happens, the coefficients are frozen in a poor state for at
least the hangover time before adaptation can be resumed.
The key to the solution is a combination of a DTD with robust statistics.
Such approach is based on introducing a scaled nonlinearity into the
adaptive algorithm. The nonlinearity limits the impact of large disturbances
on the coefficient setting, but also reduces the convergence rate. The idea
was developed for a subband echo canceller in [9].
The main objective of this work investigates the type of parameters that can
be used in robust algorithms to offer robust performance and their effect on
DT. As the performance of the robust Proportionate Affine Projection
Algorithm (PAPA) is shown to be better than other algorithms in network echo
cancellation ([3], [10], [11]), investigation is performed on the parameters
of the robust PAPA algorithm.
2. Adaptive Algorithms and Notations
In derivations and descriptions the following notations are used (see also Fig. 1).
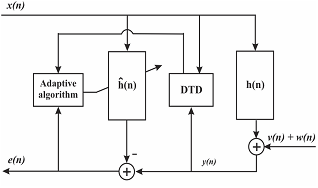
Fig. 1 Block diagram of the echo canceller and DTD [3].
The excitation vector is denoted xn=[xn,...,xn-L+1]T, where xn is the far-end speech signal. vn+ wn is the background noise mixed with the near-end speech. The microphone signal is denoted yn. The residual echo is en=yn-hnTxn, where hn=[h0,n,...,hL-1,n]T is the estimated echo path. Here L is the length of the adaptive filter.
2.1 The Proportionate Algorithms
The step-sizes in the PNLMS algorithm are calculated from the last estimate of the filter coefficients so that a larger coefficient receives a larger weight, thus increasing the convergence rate of that coefficient. This has the effect that active coefficients are adjusted faster than non active coefficients (i.e. small or zero coefficients). This algorithm is described by the following equations:
| (1) |
| (2) |
Gn is a diagonal matrix which adjusts the step-sizes, μ is the overall step-size parameter, and δ is a regularization parameter which prevents division by zero and stabilizes the solution when speech is used as input signal. The diagonal elements of Gn+1 are calculated as follows, [4],
| (3) |
| (4) |
Parameters δp and ρ are positive numbers with typical values δp = 0.01, ρ= 5/L.
A variant of this algorithm is called the PNLMS++ [5]. There, for odd-numbered time steps the matrix Gn is derived as above, while for even-numbered steps it is chosen to be the identity matrix ( Gn = I), which results in the NLMS algorithm. The alternation between NLMS and PNLMS iterations has several advantages compared to using just the PNLMS technique (in the case of pure PNLMS, as the large weights adapt, the remaining small coefficients adapt at a rate slower than NLMS), e.g., the PNLMS++ algorithm is much less sensitive to the assumption of a sparse impulse response.
2.2 The Robust NLMS and PNLMS++ Algorithms
The NLMS and PNLMS++ algorithm can both be made robust to large disturbances by modification of the criteria on which they are based [3]. The robust NLMS algorithm is given by,
| (5) |
where Ψ(.) is a limiter function,
| (6) |
and the adaptive scale factor, sn, is defined as,
| (7) |
where λ controls the scale factor. β is a normalization constant, it dependents on k0,
| (8) |
where erfc(.) is a complementary error function defined as,
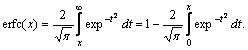 |
(9) |
As with the Geigel DTD (which is an essential component in the robust algorithms) [8], it is useful to introduce a hangover time to control scale updating. When the DTD detects DT, adaptation of sn should be inhibited for a specific time, preferably al long as the DTD hangover time, Thold, [10]:
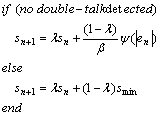 |
(10) |
The PNLMS algorithm can be made robust in an exactly analogous manner, yielding the equation
| (11) |
Alternating the iterations with Gn as given in (3) and the identity matrix then yields the robust PNLMS++ algorithm.
2.3 The Robust Proportionate APA (PAPA)
Let yn=[yn,...,yn-p+1]T, be a vector of samples yn and Xn=[xn,...,xn-L+1]T the excitation matrix, where p is the projection order. A residual echo vector en=yn-XnThn, and PAPA is then given by,
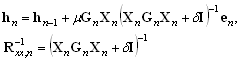 |
(12) |
where Gn is as defined in equation (2) and R
is a weighted estimate of the inverse correlation matrix of the input
signal. This matrix “whitens” the input data, Xn, and thus the
convergence rate of the adaptive filter is increased. With Gn = I
and δ=0, the equation (14)
reduces to the standard APA [6].
A robust version of PAPA (and hence of APA) is obtained straightforwardly, by applying the principles presented previously, [3]:
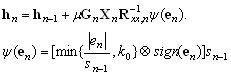 |
(13) |
where ☺ denotes elementwise multiplications and |.| in |en| operates on the individual elements.
3. Investigation of Robust Parameters
This section examines the relationship and function of the robust algorithm. In the robust PAPA Ψ(en) is an P-by-1. The scale factor sn uses the first element in the limiter matrix,
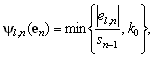 |
(14) |
| (15) |
From a glance at the equations, the parameters β and λ act as a weighting on the previous scale factor values and the current error value. This relationship between the parameters and the current error value can be demonstrated through the substitution of equation (14) into (15), yielding,
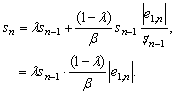 |
(16) |
If the error is small, meaning no double talk is active; the minimum function will favour the first term and this results in following equation,
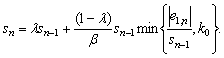 |
(17) |
From equation (17), it can be deduced that when the error is small, the
algorithm uses the previous scale factor and the current error to compute
the scale factor which will be used in the next iteration.
Similarly, when the error is large, the minimum function will favour the second term of equation (18) and the scale factor becomes,
| (18) |
In this case, the scale factor relies on the previous scale factor and k0. This implies that when DT occurs, the scale factor will use a smaller k0 value instead of the larger error value.
4. Simulations
The simulations were provided using MATLAB environment. The robust PAPA was simulated under user defined acoustic scenarios. The data used comprised of a real car channel (length of 2048 taps), female and male synthetic speech. 6 dB was used for DT as the ratio between the far-end speaker and the near-end speaker and a SNR of 20 dB was used for the noise as illustrated in Figure 2. The two main factors that were considered in the investigation of adaptive algorithms were rate of convergence and robustness.The misalignment (it was the main focus of this paper) is given by,
ε=||h-hep||/||hep||, where
hep is the true echo path. The scale estimate in (7),
sn , is never allowed to become smaller than 2. This inhibits bad behaviour in low noise situations.
The misalignment plot for k0 (Fig. 3) resulted from simulations with
k0={20,1,0.7,0.5}. As it was too large, the algorithm was not restricted and a large misalignment was observed when DT occurred. This further clarified the role of
k0 as being the restricting factor in the limiter function.
Detailed investigations were carried out to find out the effects of
β and λ using
k0 value found from the above. The parameters that were used during this section of the investigation are ,
μ=0.05,
k0=0.7, λ=0.99. For the testing of the parameter
β, the misalignment plots are illustrated in Figure 4. It is demonstrated that with increasing values of
β, the robustness of the algorithm increased.
Practical values of the robust parameters were best to be [0.99, 1) for λ in [3]. Clear the misalignment (Fig. 5) was considerably smaller when λ was large. None of the results for different λ values appeared to be severely affected by DT. However, the algorithm was more sensitive to changes for λ=0.94 and λ=0.96 since the plots diverge when the other two results did not. This corresponded to the expectations that a smaller value of λ would increase the weighting on the current values in the scale factor, thus producing a less robust solution.
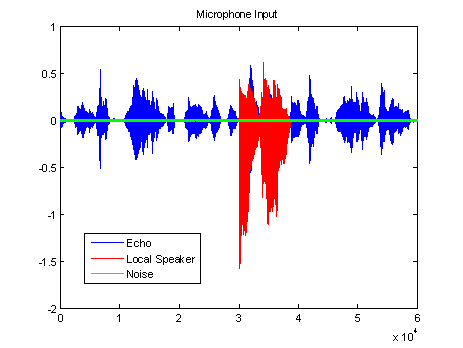
Fig. 2 Echo signal, local speaker and background noise.
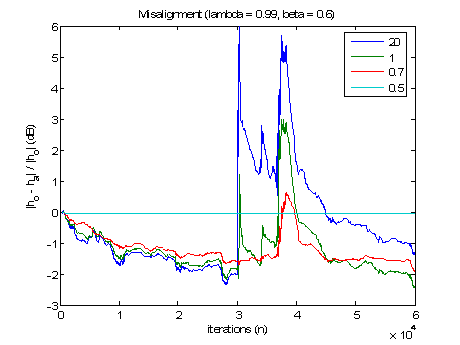
Fig. 3 Misalignment for k0.
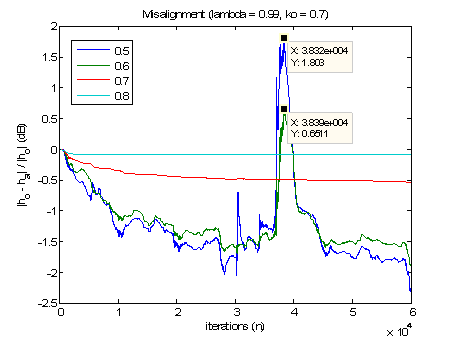
Fig. 4 Misalignment for β.
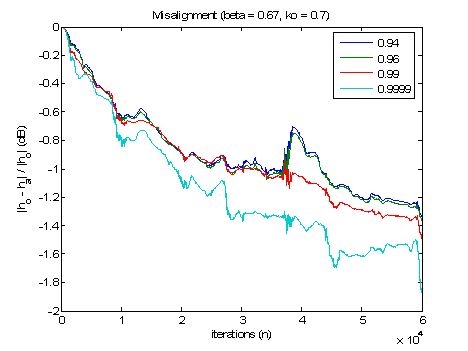
Fig. 5 Misalignment for λ.
5. Conclusion
The parameter k0 was the main robust parameter, which affected the level of divergence in the algorithm DT occurred. This parameter was the key to the limiter function, which limits the magnitude in the filter weight adaptation. The other two robust parameters β and λ could be regarded as fine-tuning parameters, which allowed users to adjust the level of robustness integral to the robust adaptive algorithms. The recommended values suggested in ([3], [10]) were found to be relevant to the acoustic environment used in the simulations. An increase in the values of β and λ was found to increase the memory of the algorithm, meaning that the algorithm demonstrated slower convergence and reacted slower to changes in the input signal. Conversely, decreasing the values of β and λ also decreased the memory of the algorithm thus allowing it to track changes more readily, as it was less robust; the algorithm was found to diverge when double-talk occurred. It was concluded that to configure the robust adaptive echo cancellation algorithms, the required degree of robustness should be known such that one can set the correct parameters. As allowing more robustness would decrease the convergence of the algorithms, it was very important to find a balance between the two key factors.
This paper has originated thanks to the support from the Ministry of Education, Youth and Sports of Czech Republic within the project MSM6840770014.
Literature
[1] C. Breining, "Control of a hands-free telephone set", Elsevier Signal
Processing, vol. 61, pp. 131-143, 1997.
[2] T. Gänsler, Benesty, J., Gay, S., Acoustic Signal Processing for
Telecommunication. Massachusetts: Kluwer Academic Publishers, 2000.
[3] T. Gänsler, J. Benesty, S. Gay, and M. Sondhi, "Double-Talk Robust Fast
Converging Algorithms for Network Echo Cancellation," IEEE Transactions on
Speech and Audio Processing, vol. 8, pp. 656-663, 2000.
[4] D. L. Duttweiler, "Proportional Normalized Least Mean Squares Adaptation
in Echo Cancellers", Lucent Bell Laboratories technical memorandum
BL01771N0-961001-01TMS, 1996.
[5] S. L. Gay, "PNLMS++ for Network Echo Cancellation", Lucent Bell
Laboratories technical memorandum BL011332-970527-04TM, 1997.
[6] K. Ozeki and T. Umeda, "An Adaptive Filtering Algorithm using an
Orthogonal Projection to an Affine Space and its Properties", Electronics
and Communications in Japan, Vol. 67-A, no. 5, 1984.
[7] S. L. Gay and S. Tavathia, "The Fast Affine Projection Algorithm", Proc.
of ICASSP, pp. 3023-3026, 1995.
[8] D. L. Duttweiler, "A twelve-channel digital echo canceler", IEEE Trans.
Commun., vol. 26, no. 5, pp. 647-653, May 1978.
[9] T. Gänsler, "A double-talk resistant subband echo canceller", Signal
Processing, vol. 65, no. 1, pp. 89-101, Feb. 1998.
[10] T. Gänsler, Benesty, J., Gay, S., Sondhi, M., "A Robust Proportionate
Affine Projection Algorithm for Network Echo Cancellation," IEEE
International Conference. Acoustics, Speech and Signal Processing, pp.
793-796, 2000.
[11] J. Huo, "Subband Acoustic Echo Cancellation," Curtin University of
Technology, 2004, pp. 1-128.
[12] S. G. Kratzer and D. R. Morgan, "The partial-rank algorithm for
adaptive beamforming", Proc. SPIE Int. Optic. Eng., Vol. 564, pp.
9-14, 1985.