Aplikace Volterrova filtru druhého řádu v kmitočtové oblasti
Autor: K. Uhlář, P. Zahradník <uhlarkam(at).fel.cvut.cz?cc=zahradni(at)fel.cvut.cz>, Pracoviště: České vysoké učení technické v Praze, FEL, Téma: Digitální zpracování signálu, Vydáno dne: 27. 11. 2009Second order Volterra filter in frequency domain
Abstract
Non-linear adaptation alogarithm can be used in telecommunication services for echo cancellation. Advantage of these algorithms is based on wide range of use for spurious systems of different property. Linear origin of disturbance represents certain subset of these systems.
Keywords: Volterra filter, second order non-linear filter
Úvod
Lineární adaptivní filtry hrají důležitou roli při potlačování akustické ozvěny v telekomunikacích a při statistickém zpracování signálů [6]. Při praktických realizacích systému však často narážíme na nelineární povahu rušení, které není možné lineárním filtrem zcela potlačit [1]. Volterrova filtrace představuje mocný nástroj pro analýzu a modelování nelineárních systému [1], [2]. Tato práce se zabývá aplikací Volterrova filtru v kmitočtové oblasti s ohledem na zlepšení rychlosti konvergence a snížení výpočetních nároků tohoto filtru. Práce vychází z algoritmu MDF [3], kde nahrazuje lineární filtry nelineárními a rozděluje kvadratický člen Volterrova filtru na sadu lineárních filtrů s nelineárním buzením. Stejným cílem, ale s jiným přístupem se podobnou problematikou zabývá práce [6]. Zde popisovaný algoritmus pracující v kmitočtové oblasti využívá cyklické konvoluce popsané v [4] s konvergenčním kritériem LMS [6]. Jedná se o blokový gradientní algoritmus [7]. Hlavní nevýhodou Volterrových filtrů s dlouhou odezvou je pomalá konvergence a citlivost ke kvantizačním chybám [2], [4]. Tato nevýhoda je potlačena použitím mnoha Volterrových filtrů s krátkou odezvou řazených v kaskádě.
Definování pojmu
Pojem „impulsová odezva“, vyskytující se v tomto textu budeme označovat impulsovou odezvu lineárního časově neměnného (LTI) systému. Pojmem „odezva“ budeme označovat odezvu nelineárního časově neměnného (NTI) systému. V anglosaské literatuře je označována jako „systém kernel“. Pro systémovou funkci platí vzah
|
| (1) |
kde reálná odezva o n proměnných
Popis filtru v časové oblasti
Volterrovy filtry patří do třídy nelineárních nerekurzivních polynomiálních filtrů [1], [2] kombinující filtry založené na rozvoji do Taylorovy řady a lineární filtry. Polynomiální filtr bez paměti reprezentovaný Taylorovou řadou lze použít např. pro modelování systémů s obecnou saturační charakteristikou [2]. Základní myšlenka Volterrova filtru vychází z definování mnoha navzájem nezávislých bloků s jedinečnou n-rozměrnou odezvou reagující na danou kombinaci vstupního signálu. Toto lze vyjádřit
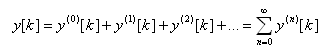 | (2) |
kde
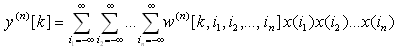 | (3) |
kde
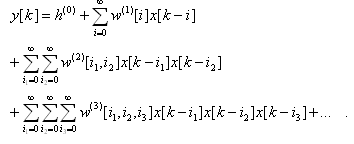 | (4) |
Pro další zjednodušení budeme předpokládat symetrii koeficientů odezvy systému,
|
| (5) |
|
| (6) |
Dalším předpokladem je omezení délky odezev jednotlivých komponent hodnotou
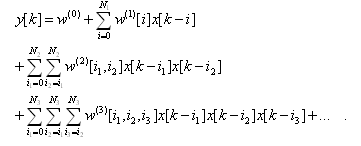 | (7) |
Popis filtru v kmitočtové oblasti
V další úvaze se omezíme na Volterrův filtr druhého řádu s vynecháním nulté komponenty a délkou odezvy systému pro oba bloky rovnou
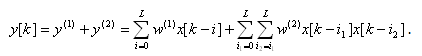 | (8) |
V kmitočtové oblasti bude obecně pro složku
|
| (9) |
Převod kvadratické složky
 |
Obrázek 1: a) Blokové schéma kvadratické komponenty Volterrova filtru pro délku odezvy L(2) = 5 v kmitočtové oblasti,
b) Rozložení koeficientů odezvy kvadratické složky filtru pro délku odezvy L(2) = 5 a zobrazení patřičného buzení.
Na obr. 1a) je zobrazeno blokové schéma kvadratické komponenty Volterrova filtru pracujícím v kmitočtové oblasti s délkou odezvy systému
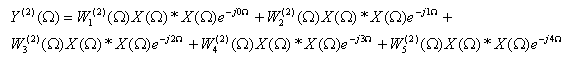 | (10) |
kde * představuje operaci cyklické konvoluce.
Systém pracující s vícenásobně zpožděným blokem dat
Filtry FLMS [4] využívají pro výpočet v kmitočtové oblasti konvolučních nebo korelačních technik označovaných v anglosaské literatuře jako “overlap-save” nebo “overlap-add” [3], [4]. Ve většině případů tvoří systém filtr s délkou impulsové odezvy danou velikostí zpracovávaného bloku vstupních dat. Takový to „dlouhý“ filtr má nevýhodné vlastnosti z hlediska citlivosti na kvantování výpočtů, rychlosti konvergence a stability systému [2]. Vylepšení rychlosti konvergence a stability přinášejí filtry MDF [3] pracujícími s mnoha krátkými lineárními filtry spojenými do jednoho bloku požadované délky impulsové odezvy. Každý filtr je v daném subbloku řízen adaptivně na daném úseku výsledné impulsové odezvy. Výsledná délka impulsové odezvy Lje daná součtem délek dílčích filtrů. Celkový počet zpožděných bloků v kaskádě je označen symbolem M. Pak pro délku FFT označenou N platí 2L/M. Hodnoty L,M volíme tak, aby byla délka filtru v daném subbloku celočíselná a měla výhodnou délku z hlediska výpočtu FFT. V prvním kroku je vstupní signál rin převeden do kmitočtové oblasti pomocí FFT
|
| (11) |
Převod (11) je proveden pouze v tomto prvním kroku a do následujících bloků je dále jen překopírováván. Ostatní kombinace vstupního signálu jako např. kvadrát či jinak posunuté násobení v kvadratické složce filtru je prováděno pouze v kmitočtové oblasti. Pro výstupní chybový signál platí
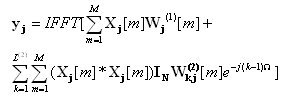 | (12) |
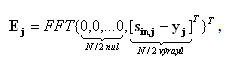 | (13) |
kde W[m,j] je vektor koeficientů odezvy, yj uvedené ve vztahu (13) je omezeno na délku (N/2,N> a Sin,j představuje signál po průchodu rušivou soustavou v časovém okamžiku j. Z LMS kritéria pro výpočet korekce váhovacích koeficientů odezvy Volterrova filtru platí
|
| (14) |
|
| (15) |
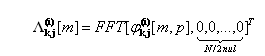 | (16) |
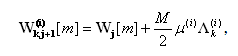 | (17) |
kde
 |
Obrázek 2: a) Blokové schéma adaptivního Volterrova filtru realizovaného pomocí mnoha krátkých zpožděných bloků v kmitočtové oblasti, kde S/P je sériově paralelní a P/S je paralelně sériový převodník, b) Obecné schéma systému pro potlačování akustické ozvěny v telekomunikační technice, c) Proměnné vstupující/vystupující do/z jednotlivých adaptivních bloků.
Každý Volterrův filtr z blokového schématu na obr. 2a představuje výpočet jednoho sloupce koeficientů kvadratické odezvy systému zobrazené na obr. 3. První filtr představuje výpočet koeficientů pro kombinace bloků (MxM, Mx(M-1), ..., Mx1), druhý filtr pro kombinace ((M-1)x(M-1), (M-1)x(M-2), ..., (M-1)x1), atd. Celkový počet bloků potřebných pro výpočet všech koeficientů odezvy systému je
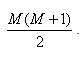 | (18) |
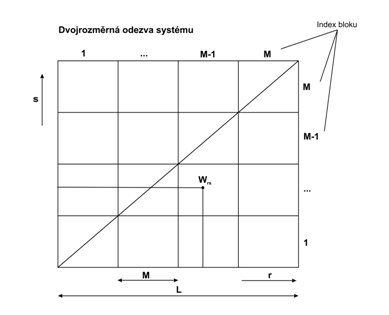 |
Obrázek 3: Rozdělení dvojrozměrné odezvy Volterrova filtru na jednotlivé subbloky a jejich indexace. Délka odezvy systému je označena symbolem L, délka subbloku M. Indexy r a s jednoznačně určují daný koeficient odezvy systému W.
Simulace
V simulaci je porovnávána výše navržená bloková struktura filtru pracujícím v kmitočtové oblasti s délkou odezvy systému L=128 a M=24 se stejným filtrem pro L=128 a M=24. Vstupní signál má vlastnosti normálního rozdělení se směrodatnou odchylkou
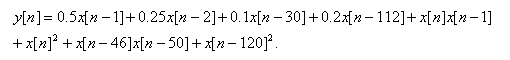 | (19) |
Rovnici rušivé soustavy lze zvolit libovolně při dodržení podmínky celkové délky odezvy systému a použitím nejvýše kvadratických členů. Pro výpočet výsledných konvergenčních charakteristik je použit algoritmus používající normalizovanou střední kvadratickou odchylky pruměrovanou přes deset nezávislých měření v dB danou
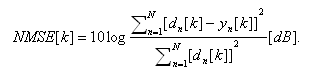 | (20) |
Na obr. 4 jsou zobrazeny konvergenční charakteristiky daných adaptivních filtrů. Při použití kratšího bloku je patrná rychlejší konvergence výsledného filtru, kterou zajišťuje koeficient M/2 (násobící konstanta) v rovnici (17). Při použití stejné hodnoty násobící konstanty vypočtené s použitím krátkých filtrů pro dlouhé filtry bude tato adaptivní soustava vykazovat vysokou míru divergence. Násobící konstanta M/2 byla stanovena experimentálně za použití simulací pro normální rozdělení vstupního signálu se směrodatnou odchylkou
 |
Obrázek 4: Konvergenční charakteristika výsledného adaptivního filtru popsaného na obr. 2a pro různý počet vnitřních bloků.
Závěr
Použití Volterrova filtru druhého řádu v kmitočtové oblasti přináší nové možnosti při potlačování akustické ozvěny v telekomunikacích. Kvadratická komponenta sleduje další nelineární vazby rušivé soustavy, které dokáže lépe aproximovat a tedy i lépe potlačit. Použití blokové struktury přináší zlepšení rychlosti konvergence a zvýšení stability celé soustavy v důsledku použití kratších filtrů. Krátké vstupní bloky také snižují velikost zpoždění danou S/P převodníkem na vstupu soustavy. Další krok bude zaměřen na zjednodušení výpočtu aktualizace jednotlivých koeficientů odezvy Volterrova filtru. Tato výpočetní náročnost roste exponenciálně s délkami filtrů v jednotlivých složkách a s počtem těchto složek.
Poděkování
Tato práce byla podpořena výzkumným záměrem Výzkum perspektivních informačních a komunikačních technologií MSM6840770014.
Reference
[1] A. Borys, “Discrete Volterra Series and Nonlinear Echo Cancellation”, Book, CRC Press LLC, London, 2001.
[2] F. Kuch, “Adaptive Polynomial Filters and their Application to Nonlinear Acoustic Echo Cancellation”, Doktor-Ingenieur, Der Technischen Fakultat der Friedrich-Alexander-Universitat Erlangen-Nurumberg zur Erlangung des Grades, Erlangen, 2005.
[3] J. Sien, K.K. Pang, “Multidelay Block Frequency Domain Adaptive Filter”, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 38, pp. 373-376, No. 2, February 1990.
[4] J.J. Shynk, “Frequency-Domain and Multirate Adaptive Filtering”, IEEE SP MAGAZINE, pp. 1-37, January, 1992.
[5] M. Zeller, W. Kellermann, “Fast Adaptation of Frequency-domain Volterra Filters Using Inherent Recursions of Iterated Coefficient Updates”, University of Erlangen-Nuernberg, EURASIP, 2007.
[6] F. Kuech, W. Kellermann, Member, IEEE, “Partioned Block Frequency- Domain Adaptive Second-ord Volterra Filter”, IEEE Transactions on Signal Processing, Vol. 53, No. 2, February 2005.
[7] J. Uhlíř, P. Sovka, “Číslicové zpracování signálů”, Vydavatelství ČVUT, Praha 2002, ISBN 80-01-02613-2.