Možnosti využitia výpočtov na GPU pri simulácii posluchového priestoru
Autor: K. Orlovský <xorlov00(at)stud.feec.vutbr.cz>, Pracoviště: Vysoké učení technické v Brně, Téma: Elektronika a audio, Vydáno dne: 03. 09. 2012Abstract
The principle of the simulation of sound source propagation in closed auditory spaces is described in this article. Moreover, the article proposes one possible algorithm for computing closed auditory space parameters, such as impulse response, frequency characteristic and reverberation time. The alrticle also elaborates on possibilities of parallelization of this algorithm and its application on GPU. Finally it compares time complexity of this algorithm running with varying number of threads.
Keywords: auditory space simulation, Image Source method, Ray-Tracing method, GPU
Úvod
V dnešnej dobe sa pri návrhu uzavretých priestorov (obzvlášť určitých typov priestorov, ako sú posluchárne, auly, konferenčné sály a pod.) stále častejšie berie ohľad aj na akustické vlastnosti daného priestoru. Jedná sa najmä o dobu dozvuku, impulzovú odozvu a niekedy aj frekvenčne závislý útlm priestoru. Na základe týchto vlastností tak môžeme sledovať a modelovať akustické vlastnosti posluchového prostredia ešte pred jeho samotnou realizáciou. Výpočet týchto vlastností je však pomerne náročná záležitosť vzhľadom na zložitosť šírenia zvuku v uzavretom priestore. Pre samotný výpočet existujú dva modely. Jedným je model výpočtu pomocou vlnovej rovnice. V tomto článku však budeme popisovať výpočet týchto vlastností pomocou prostriedkov geometrickej akustiky, ktorá nám umožňuje simulovať šírenie zvuku v priestore, zvukové odrazy, difúzne odrazy a takisto difrakciu zvukovej vlny. Tento článok popisuje možnosti paralelizácie jednotlivých krokov, z ktorých tento výpočet pozostáva. Bežné procesorové jednotky (CPU) sú stavané ako sériové a vykonávajú operácie sekvenčne. Ich výkon časom narastal so vzrastajúcou taktovacou frekvenciou. Tie však postupne narazili na hranicu možností. Preto sa zvolila nová cesta zvyšovania výkonu a to cesta násobných jadier procesorovej jednotky. Tu takisto poznáme dva smery, kam viedol vývoj architektúry multiprocesorových jednotiek. Jedná sa o multiprocesorové jednotky obsahujúce niekoľko výkonných jadier (napríklad architektúra Core od firmy Intel) [1]. Druhým smerom vývoja sú procesorové jednotky s vysokým počtom (desiatky až stovky) jadier, ktoré kombinujú jemné a hrubé paralelizovanie. K týmto architektúram patria najmä grafické procesorové jednotky (GPU). Tieto grafické procesorové jednotky sa v niektorých smeroch vyznačujú oveľa vyšším výkonom ako klasické CPU. Takisto sú GPU stavané ako výpočtová jednotka pre množstvo dát, ktoré sa spracúva rovnako. V praxi sa za posledných niekoľko rokov začal využívať výpočtový potenciál GPU pre rôzne vedecké, databázové, geometrické a iné výpočty [1]. Tieto ich vlastnosti sa dajú s výhodou využiť pre výpočty geometrickej akustiky, čo popisujeme v ďalších kapitolách článku. Samotný článok popisuje možnosti paralelizovania jednotlivých krokov výpočtu, ktoré tak vedie k jeho urýchleniu a takisto aj efektívnejšiemu využitiu dostupných výpočtových prostriedkov. V prvej kapitole je navrhnutý algoritmus, ktorý by realizoval auralizáciu posluchového priestoru pomocou prostriedkov geometrickej akustiky. Druhá kapitola potom rozoberá možnosti paralelizácie jednotlivých krokov výpočtu. Tretia kapitola popisuje výsledky pre simulácie realizované v prostredí MATLAB. v poslednej kapitole popisujeme možnosti paralelných výpočtov pomocou GPU.
Simulovanie šírenia zvukovej vlny
Táto kapitola popisuje princíp šírenia zvukovej vlny v uzavretom priestore, ktorý môžeme rozdeliť do niekoľkých základných krokov popísaných blokovou schémou na obrázku 1:
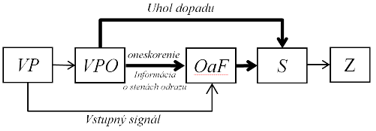
Obr. 1 Bloková schéma algoritmu pre simulovanie šírenia zvukovej vlny v uzavretom posluchovom priestore.
Prvým krokom algoritmu popísaného blokovou schémou na obrázku 1 je voľba parametrov pravouhlej miestnosti (blok VP). Tu si volíme jej rozmery, umiestnenie zdroja zvuku a poslucháča a takisto materiál jednotlivých stien. Takisto si tu môžeme vybrať medzi 2D a 3D simuláciou. Pre takto navrhnutú topológiu miestnosti sa v druhom kroku (blok VPO- výpočet parametrov odrazov) realizuje výpočet parametrov zvukových vĺn, ktoré dopadajú k poslucháčovi ako odrazené od stien miestnosti. Jeho výsledkom je uhol dopadu zvukovej vlny, vzdialenosť, ktorú vlna musí uraziť k poslucháčovi a informácia o stenách, ktorými sa táto zvuková vlna musela odraziť, aby dosiahla poslucháča. Výpočet týchto informácií je možné realizovať rôznymi metódami, ako je obrazová metóda [2, 3, 4] alebo metóda ray-tracing [4, 5] a pod. V ďalšom bloku realizujúcom oneskorenie a filtráciu (blok OaF) sa vytvorí impulzová odozva pre každý simulovaný odraz. Takto získané impulzové odozvy jednotlivých zvukových odrazov sa ďalej spracúvajú v bloku S (spracovanie) podľa požadovaného zobrazovaného výstupu (Z- zobrazenie) danej simulácie.
Možnosti paralelizácie algoritmu
Ako bolo popísané v kapitole č. 2, samotný algoritmus pozostáva z niekoľkých krokov výpočtu. Na začiatku sa stanovia parametre miestnosti. Na základe nich sa potom vypočítavajú zvukové vlny, ktoré dorazia k poslucháčovi. Tento krok môže byť realizovaný rôznymi metódami. Najznámejšími sú metóda ray-tracing a obrazová metóda (image source method). Existuje aj niekoľko ďalších metód, ktoré sú odvodené od týchto metód. Zameriame sa však len na tieto dve základné metódy.
Výpočet parametrov odrazov zvukovej vlny
Obrazová metóda je jednoduchá metóda, ktorá umožňuje výpočet parametrov dopadu zvukovej vlny k poslucháčovi po jej odrazení od jednej, či viacerých stien posluchového priestoru. Je to efektívna a účinná metóda, čo znamená, že nájde všetky odrazené zvukové vlny do zvoleného kritéria. Princíp metódy spočíva v reprezentovaní zvukovej vlny odrazenej od stien miestnosti, ako priamky, spájajúcej virtuálny zdroj zvuku umiestnený vo virtuálnej miestnosti s poslucháčom [4]. Túto situáciu bližšie popisuje obrázok 2. Polohy jednotlivých virtuálnych zdrojov potom nájdeme odrážaním všetkých zdrojov zvuku (reálneho aj virtuálnych) cez všetky odrazivé plochy (v tomto prípade steny miestnosti) do zvoleného kritéria. Tým je dosiahnutie maximálnej vzdialenosti virtuálneho zdroja zvuku od poslucháča. Tento algoritmus je rekurzívny. Odrážanie virtuálneho zdroja cez steny vytvorí nové virtuálne zdroje, ktoré sa následne odrážajú ďalej cez všetky steny [4].

Obr. 2 Znázornenie princípu výpočtu vzdialenosti, ktorú musí prekonať zvuková vlna na ceste od reálneho zdroja zvuku (RZ) ku poslucháčovi (P) pomocou virtuálneho zdroja zvuku (VZ) nájdeného zrkadlením cez stenu.
Metóda Ray-Tracing je v praxi využívaná častejšie, pretože oproti obrazovej metóde je jej použitie pri zložitých tvaroch posluchových priestorov jednoduchšie. V metóde ray-tracing je emitovaný konštantný počet lúčov do rôznych smerov priestoru s rovnakým uhlom od daného zdrojového bodu (zdroja zvuku). Každý lúč je naťahovaný pomocou lineárnej extrapolácie a zrkadlového odrazu, kým nedosiahne okolie poslucháča (obrázok 3) [4].

Obr. 3 Princíp vyhľadávania odrazov metódou ray-tracing. Od zdroja zvuku (Z) sa vyhľadávajú cesty k poslucháčovi (P) pomocou tzv. lúčov.
Sledujú sa trasy týchto lúčov a tie strácajú svoju energiu s každým odrazom podľa absorpčných koeficientov povrchov daných stien. Keď lúče zasiahnu povrch steny, ich nový smer sa vypočíta podľa Snellovho zákona [4]:

kde θd predstavuje uhol dopadu a θo predstavuje uhol odrazu zvukovej vlny ku kolmici na rovinu dopadu. Metóda ray-tracing obmedzuje svoj výpočet predpokladom, že zdroj vysiela konečný počet lúčov rovnomerne rozptýlených všetkými smermi. Výsledkom toho je, že táto metóda vždy nájde stanovený počet zvukových ciest, ale tie nebudú nevyhnutne všetkými odrazmi v stanovenom časovom rozpätí [4].
Pri porovnávaní týchto metód sa zameriame hlavne na možnosť paralelizácie ich algoritmu. Obrazovú metódu by sme mohli nazvať “hierarchickou“. A to z dôvodu, že na nachádzanie virtuálnych zdrojov zvuku o rád vyššie musíme poznať polohu všetkých virtuálnych zdrojov zvuku aktuálneho rádu (vyplýva z princípu metódy). To znamená, že táto metóda je síce paralelizovateľná, avšak jednotlivé vlákna algoritmu (resp. hierarchie tejto metódy) dospejú k niektorým zhodným výsledkom nezávisle na sebe, čo sa musí nasledne korigovať. V opačnom prípade by boli niektoré zdroje zvuku (v našom prípade zvukové odrazy) reprezentované duplicitne. Naproti tomu metóda ray-tracing je paralelizovateľná pomerne jednoducho, keďže sa jedná len o vysielanie samostatných lúčov, ktoré nezávisia jeden na druhom. Každé vlákno algoritmu by spracovávalo jeden lúč, ktorý by potom vyhodnotilo a v prípade, že by dosiahol poslucháča, tak sa parametre toho zvukového odrazu uložia.
Oneskorenie zvukovej vlny a filtrácia
Táto časť algoritmu vytvára signál danej zvukovej vlny na základe vstupného signálu a vypočítaných parametrov odrazov danej miestnosti. Prakticky sa tu realizuje oneskorenie vstupného signálu a jeho filtrácia. Oneskorenie signálu závisí na absolútnej vzdialenosti, ktorú musí zvuková vlna uraziť od zdroja zvuku, aby dosiahla poslucháča podľa vzťahu [6]:

kde l je vzdialenosť urazená zvukovou vlnou, c je rýchlosť zvuku v danom priestore a fvz je vzorkovacia frekvencia vstupného monofónneho zvukového signálu. Zátvorky značia zaokrúhlenie na celé číslo smerom nahor. Takto získame časové rozdiely medzi jednotlivými zvukovými vlnami prichádzajúcimi do ľudského ucha. Filtráciou vstupného signálu príslušnými filtrami dosahujeme potrebné frekvenčné obmedzenie v určitých pásmach, čím sa napodobní frekvenčne závislá zvuková pohltivosť daného materiálu, ktorým je tvorená stena miestnosti. Samotná filtrácia môže byť realizovaná v časovej oblasti (FIR alebo IIR filter) alebo frekvenčnej oblasti (pomocou Fourierovej transformácie). Oba tieto prípady je možné paralelizovať. Navrhovaný algoritmus využíva na filtrovanie vstupného signálu navrhnuté IIR filtre. Samotná koncepcia je taká, že algoritmus realizuje niekoľko vlákien pre spracovávanie vstupného signálu, pričom tieto vlákna pracujú sekvenčne a v každom vlákne sú realizované samostatné IIR filtre (nejedná sa o paralelne realizovaný jeden IIR filter, ale o paralelne pracujúcu skupinu samostatných filtrov) Súčasťou filtrovania vstupného signálu je aj úprava jeho intenzity s ohľadom na vzdialenosť, ktorú by musela zvuková vlna uraziť od zdroja zvuku k poslucháčovi v danom simulovanom uzavretom prostredí podľa vzťahu [6]:

kde Lp je hladina poklesu intenzity zvuku v dB pre daný zvukový odraz, ktorý musí ku poslucháčovi uraziť vzdialenosť r2 . Ako referenčná vzdialenosť (r1) je zvolená vzdialenosť 1m. Vstupný monofónny signál tak figuruje ako signál s intenzitou, ktorá by bola nameraná vo vzdialenosti 1m od tohto zdroja zvuku. Preto môžeme tento vzťah zjednodušiť na:

Pri uvážení, že jednotlivé odrazy sa musia filtrovať toľko krát, koľko krát by sa musela odraziť daná zvuková vlna stenami, kým by dorazila k poslucháčovi, je práve táto časť navrhnutého algoritmu výpočtovo najnáročnejšia. Avšak túto vpočtovú náročnosť je možné eliminovať paralelizovaním procesov tohto kroku. Spracovanie jednotlivých zvukových vĺn je takisto na sebe nezávislé. Nepotrebujeme poznať dielčie výsledky spracovania jednotlivých zvukových vĺn, aby sme mohli spracúvať ďalšie. Preto sa v tomto kroku môžu jednotlivé zvukové vlny spracúvať viacerými vláknami algoritmu. Vo výsledku sa potom jednotlivé zvukové vlny sčítajú, čím vznikne výsledná zvuková vlna.
Možnosti paralelizácie algoritmu
Ako bolo spomenuté v úvode, GPU ponúka vysoký výpočtový výkon a takisto vysoký stupeň paralelizácie výpočtov vďaka vysokému počtu nezávislých výpočtových jadier. Ich základom je SIMD (Single Instruction- Multiple Data) technológia výpočtov, ktoré umožňujú spracúvať viacero prúdov dát rovnakými inštrukciami. V oblasti geometrickej akustiky môže byť paralelizovaných viacero operácií. V ďalších odsekoch sa však zameriame na tieto tri operácie, ktoré sú často potrebné pre modelovanie posluchového priestoru [1]:
• geometrické operácie
• konvolúcia
• vlnovo orientované výpočty difrakcie
Implementácia algoritmu ray-tracing pre výpočet parametrov zvukových odrazov na GPU môže poskytnúť značné výhody a úsporu času. Výpočet algoritmom ray-tracing vo vizuálnej oblasti bol jedným z prvých, ktorým bolo možné využiť výhody paralelizácie na GPU [7]. Počas posledných rokov sa obnovila pozornosť vo vývoji rýchlych algoritmov ray-tracing pre GPU [8]. Tie isté princípy sú aplikovateľné takisto pre algoritmus ray-tracing používaný v akustickej oblasti. Všetky systémy založené na metóde ray-tracing využívajú v praxi nejaké informácie o štruktúre priestoru na rozdelenie priestoru do menších častí, alebo použtie hierarchicky ohraničených častí. Tieto hierarchické dátové štruktúry môžu byť pre dynamické scény počítané takisto paralelnou GPU architektúrou [9,10]. To predpokladá, že je možné redukovať počet potrebných výpočtov priesečníkov lúčov s mnohouholníkmi tvoriacimi priestor [1]. Frekvenčne orientovaný akustický prenos vyžarovania je technikou vhodnou pre auralizáciu v reálnom čase [11]. Počet potrebných operácií konvolúcie v tejto metóde je pozoruhodný pri komplexných modeloch. Obe sú potrebné pri prevode energie medzi povrchovými časťami a pri auralizácii. Výpočtovo je výhodné vykonávať tieto operácie vo frekvenčnej oblasti, keďže v tejto oblasti je konvolúcia len násobením dvoch vektorov a tým je úplne paralelizovateľná pre implementáciu na GPU [1].
Príklady simulácie v prostredí MATLAB
Na základe poznatkov uvedených v predchádzajúcich kapitolách boli v prostredí Matlab vytvorené simulácie s cieľom preskúmať efektivitu paralelizácie spracovania signálu jednotlivých zvukových vĺn popísaných v kapitole 3.2 (Oneskorenie zvukovej vlny a jej filtrácia). Bola vytvorená aplikácia pre simuláciu posluchového prostredia s vlastným GUI, kde bolo možné nastavovať všetky parametre simulácií a takisto zobrazovať výsledky simulácií. Pre jednoduchosť pracovala táto aplikácia s miestnosťou pravouhlého tvaru, v ktorej neboli žiadne prekážky. Aplikácia umožňovala na základe známych rozmerov miestnosti, polôh poslucháča a zdroja zvuku a takisto na základe zvolených materiálov jednotlivých stien miestnosti vypočítavať impulzovú odozvu pre šírenie zvukovej vlny od zdroja zvuku ku poslucháčovi a takisto aj frekvenčnú charakteristiku zvukovej vlny dopadajúcej k poslucháčovi. Takisto vypočítavala teoretické odhady doby dozvuku v tejto miestnosti podľa Sabina, Eyringa a Milingtona. Pri simulácii sa meral čas trvania spracovávania jednotlivých zvukových vĺn popisaného v kapitole 3.2 (Oneskorenie zvukovej vlny a jej filtrácia). Súčasťou merania nebol výpočet parametrov týchto zvukových vĺn, ktoré sa vypočítavali pomocou obrazovej metódy. Pri meraní sme využívali aplikáciu popisovanú v tejto kapitole, ktorá bola navrhnutá a naprogramovaná v prostredí MATLAB 2011b. Na simulovanie sa použil výkonný desktopový počítač s procesorom Intel Core i7 960. Tento procesor poskytuje 4 fyzické jadrá a spolu 8 logických jadier pracujúcich na taktovacej frekvencii 3,20 GHz. Počítač bol vybavený 12GB RAM.

Obr. 4 GUI navrhnutej aplikácie.
Simulácie prebiehali sekvenčne pre rôzny počet jadier CPU, ktoré sa do výpočtu zapájai a takisto pre rôzne množstvo dát, čiže rôzny maximálny rád odrazov. Meral sa čas spracovávania signálu zvukových vĺn dopadajúcich k poslucháčovi. Simulácie sa vykonávali bezprostredne po sebe a topológia miestnosti sa nemenila. Aby sa predišlo náhodným chybám, bola každá simiulácia (pre konkrétny počet jadier a pre konkrétny maximálny rád odrazu) vykonaná 100 krát. Samotné spracovanie výsledkov však prebiehalo bez 1. a 3. kvartilu (25% najmenších časov a 25% najväčších časov sa nebralo do úvahy). Časový priemer sa tak počítal len z 50 nameraných časov, ktoré ležali v rozmedzí centrálnych 50% hodnôt. Aritmetický priemer časov nameraných pre jednotlivé simulácie uvádza tabuľka č. 1.
Tabuľka 1: Výpočtový čas simulácií.

Grafické znázornenie týchto hodnôt môžeme vidieť na obrázku č. 5.

Obr. 5 Grafické znázornenie času výpočtu simulácií v závislosti na počte použitých výpočtových jadier CPU pre rôzny maximálny rád odrazu.
Z nameraných údajov môžeme konštatovať, že paralelizácia podstatne znižuje potrebný čas výpočtu. Obzvlášť pri väčšom množstve dát je čas potrebný pre výpočet približne 2 – 3 krát menší. Z obrázka je takisto zrejmé, že zvýšenie počtu zapojených jadier sa prejaví viac pri väčšom množstve spracúvaných dát.
Záver
Auralizáciu virtuálneho priestoru je možné realizovať pomocou paralelných výpočtov, čo značne urýchli samotný algoritmus bez jeho závažných zmien. Dokazuje to aj navrhnutý algoritmus pre simuláciu posluchového prostredia, keďže paralelizovaním jeho jednotlivých krokov dochádza k značnej úspore času potrebného pre spracovanie dát. Ako vyplýva zo simulácií (obrázok 5), aplikovanie algoritmu na viacero jadier CPU podstatne znižuje potrebný čas výpočtu. Obzvlášť pri väčšom množstve dát je čas potrebný pre výpočet približne 2 – 3 krát menší. Ďalšie možnosti zrýchlenia tohto algoritmu sú popísané v kapitole 5, ktorá uvádza možnosti aplikovania tohto algoritmu na GPU. Tie v dnešnej dobe poskytujú vysoký výpočtový výkon vďaka vysokej možnosti paralelizácie procesov na nich a taksito aj vďaka jej architektúre, ktorá umožňuje jednuduchú implementáciu niektorých algoritmov pre paralelné spracovanie dát, ako je napr. metóda ray-tracing. Na základe týchto poznatkov a skúseností je možné vývojom hardwaru a novými algoritmami dosiahnuť spracovávanie týchto údajov v reálnom čase aj pre zložitejšie tvary posluchových priestorov.
Literatúra
[1] Savioja L.; Manocha D.; Lin M. C., “Use of GPUs in room acousticmodeling and auralization,” in Proc. Int. Symp. Room Acoustics, Aug 2010.
[2] Allen, J. B.; Berkley, D. A., “Image method for efficiently simulating small-room acoustics,” The Journal of the Acoustical Society of America, vol. 65, no. 4, pp. 943–950, Apr. 1979.
[3] Viveiros, E. B., Gibbs, B. M., “An image method for predicting the field performance of acoustic louvres from impulse response measurements.” Applied Acoustics, vol. 64, pp. 713–730, 2003.
[4] Borish, J., “Extension of the image model to arbitrary polyhedra,” The Journal of the Acoustical Society of America, vol. 75, no. 6, pp. 1827–1836, 1984.
[5] Krokstad, A.; Strom, S.; Sorsdal, S., “Calculating the acoustical room response by the use of a ray tracing technique,” Journal of Sound and Vibration, vol. 8, no. 1, pp. 118–125, 1968.
[6] Olovsky, K.; Balik, M., “Panoramovanie zdroja zvuku s možnosťou zmeny jeho zdanlivej vzdialenosti.” Elektrorevue - Internetový časopis (http://www.elektrorevue.cz), vol. 63, pp. 1–12, 2011.
[7] Carr, N.; Hall, J.; Hart, J., “The ray engine,” in Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, ser. HWWS ’02, 2002, pp. 37–46.
[8] Popov, S.; Gnther, J.; Seidel, H.; Slusallek, P., “Stackless kd-tree traversal for high performance gpu ray tracing.” Comput. Graph. Forum, vol. 26, no. 3, pp. 415–424, 2007.
[9] Zhou, K.; Hou, Q.; Wang, R.; Guo, B., “Real-time kd-tree construction on graphics hardware,” ACM Trans. Graph., vol. 27, no. 5, pp. 126:1–126:11, Dec. 2008.
[10] Lauterbach, C.; Garland, M.; Sengupta, S.; Luebke, D. ; Manocha, Q. D.;, “Fast bvh construction on gpus.” Comput. Graph. Forum, vol. 28, no. 2, pp. 375–384, 2009.
[11] Siltanen, S.; Lokki, T.; Savioja, L., “Frequency domain acoustic radiance transfer for real-time auralization,” Acta Acustica united with Acustica, vol. 95, no. 1, pp. 106–117.