Modely symetrických vedení založené na fyzikálních vlastnostech a geometrii kabelu

Článek popisuje a srovnává dva modely symetrických vedení. Tyto modely vycházejí z geometrických rozměrů přenosového média a jeho fyzikálních vlastností (skin efekt, jev blízkosti). První model má svůj původ v teorii elektromagnetického pole a je založen na použití Besselových funkcí, druhý je empirický.

---

Models of symmetrical twisted pairs - based on geometrical size of transmission media and its physical features

Abstract

This article describes and compares two models of symmetrical twisted pairs. Those models are based on geometrical size of transmission media and its physical features (skin effect, effect of closeness). First model has its bases in electromagnetic field and uses Bessel function, second one is empirical.

---

Jak ukazuje dostupná literatura, je možné provádět simulace sekundárních parametrů symetrických vedení (např. pomocí modelů, které byly navrženy společnostmi Deutsche Telekom AG Company či Royal PTT Netherlands) nebo simulovat přímo primární parametry (jak to provádí například British Telecom). Další možností je použít některé z modelů, které vycházejí z fyzikálních vlastností vedení a geometrie kabelů. Z těchto modelů je možné sledovat změny parametrů vedení v závislosti na frekvenci a určit, zda modelovaný typ kabelu je vhodný pro nasazení určitého druhu přenosového systému - např. na bázi digitálních účastnických přípojek xDSL.

Fyzikální model založený na využití Besselových funkcí

Účastnická metalická vedení jsou popsána parciálními diferenciálními rovnicemi druhého řádu s konstantními koeficienty zvanými telegrafní rovnice:

(1)

(2)

Odvození telegrafní rovnice vychází z aplikace Kirhoffových zákonů na náhradní schéma homogenního vedení.

Obr. 1 Náhradní schéma elementu homogenního vedení

Dále pro homogenní vedení platí tzv. rovnice skinefektu (povrchového jevu):

(3)

kde Δ je Laplaceův operátor, J představuje vektor proudové hustoty, μ je magnetická permeabilita a ρ je elektrická rezistivita. Pokud uvažujeme harmonické změny a ustálený stav, platí:

(4)

Bude-li proud protékat ve směru osy z, je J=(0,0,J_z) a rovnice (4), vyjádřená v cylindrických souřadnicích, přejde na tvar:

(5)

Rovnice (5) představuje Besselovu rovnici, jejímž řešením jsou Besselovy funkce.

Model založený na využití Besselových funkcí je součástí doporučení ITU-T G.996.1, které se zabývá zkušebními postupy pro DSL transceivery. Primární parametry jsou ovlivněny geometrickými parametry jako jsou průměr jádra a žíly, tloušťka izolace, typ kabelového prvku apod. a dále použitým materiálem vodiče a izolace.

Pro měrný odpor R a indukčnost L izolovaného symetrického páru platí:

[Ω/m]

(6)

resp.

[H/m]

(7)

kde R_i a L_i jsou zapříčiněny povrchovým jevem, R_n a L_n jsou důsledkem vířivých proudů uvnitř páru (jev blízkosti). L_a je vnitřní indukčnost.

Výše popsané veličiny jsou dány těmito vztahy:

[Ω/m]

(8)

[Ω/m]

(9)

[H/m]

(10)

[H/m]

(11)

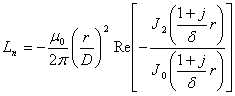[H/m]

(12)

kde ρ je elektrická rezistivita [Ω.m], r je poloměr jádra [m], μ₀ je magnetická permeabilita vakua [H/m], μ_r je relativní permeabilita vodiče. D je středová vzdálenost vodičů [m] a J₀, J₁, J₂ jsou nultý, první a druhý řád Besselovy funkce prvního druhu. Veličina δ je hloubka vniku elektromagnetické vlny:

[m]

(13)

kde ω je úhlová frekvence [rad.s^-1].

Výraz (1+j)⁄δ přestavuje konstantu τ uvedenou v (5). Odvození lze nalézt např. v [4].

Empirický model

Tento model podle [1] využívá sadu rovnic, jejichž použitím se lze vyhnout Besselovým funkcím. Pro výpočet měrného odporu i měrné indukčnosti je nutné nejprve určit stejnosměrný odpor smyčky R₀:

[Ω/m]

(14)

Z (14) je patrné, že v (8) první činitel součinu představuje stejnosměrný odpor jednoho vodiče. Zbytek výrazu pak odpovídá impedanci způsobené povrchovým jevem. Podobně (9) lze rozdělit na pomyslný stejnosměrný odpor (s poloměrem rovným vzdálenost mezi vodiči) a impedanci způsobenou jevem blízkosti.

S ohledem na povrchový jev je stanoven bezrozměrný parametr w (tzv. normalizovaná frekvence) v závislosti na poloměru jádra, rezistivitě a permeabilitě:

[-]

(15)

Z (15) je zřejmá souvislost mezi normalizovanou frekvencí u empirickém modelu a hloubkou vniku (13) u modelu s Besselovými funkcemi:

[-]

(16)

Výsledný měrný odpor R a vnitřní měrnou indukčnost L₀ lze získat z následujích vztahů:

[Ω/m]

(17)

resp.

[H/m]

(18)

Celková měrná indukčnost L je poté dána rovnicí:

[H/m]

(19)

kde H je bezrozměrný geometrický faktor závisející na uspořádaní vodičů v kabelu. Pro symetrický pár je:

[-]

(20)

Z dosazení předchozí rovnice do (16) tedy plyne, že:

[H/m]

(21)

Obr. 2 a 4 ukazují v pásmu 100 kHz - 100 MHz průběhy měrného odporu a měrné indukčnosti symetrického páru s průměrem jádra d = 0,4 mm a různými poměry d/D: 0,44; 0,50; 0,57; 0,67; 0,80. (žíla z Cu, izolace z pevného PE). Jelikož na obr.1 není patrný rozdíl mezi oběma modely, je na obr. 2 zobrazen detail v oblasti 50 - 60 MHz.

Obr. 2 Průběhy měrného odporu v závislosti na poměrech d/D

Obr. 3 Detail průběhů měrného odporu v závislosti na poměrech d/D

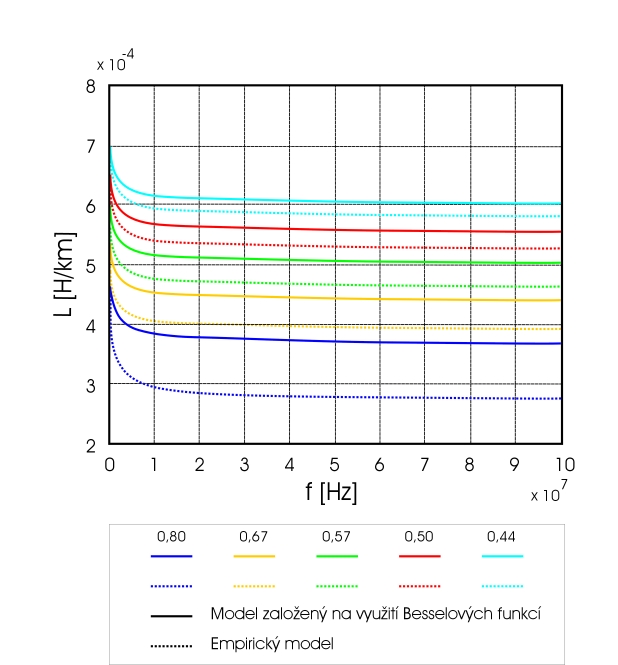
Obr. 4 Průběhy měrné indukčnosti v závislosti na poměrech d/D

Obr. 5 a 6 porovnává empirický model měrného odporu resp. indukčnosti se skutečným průběhem, jenž byl měřen spektrálním analyzátorem Rohde & Schwarz ZVRE. Jedná se o telekomunikační kabel čtyřkové konstrukce s polyethylenovou izolací, průměrem jádra 0.4 mm a průměrem žíly 0.6 mm. Tento kabel je nejpoužívanějším médiem v přístupové síti Českého Telecomu.

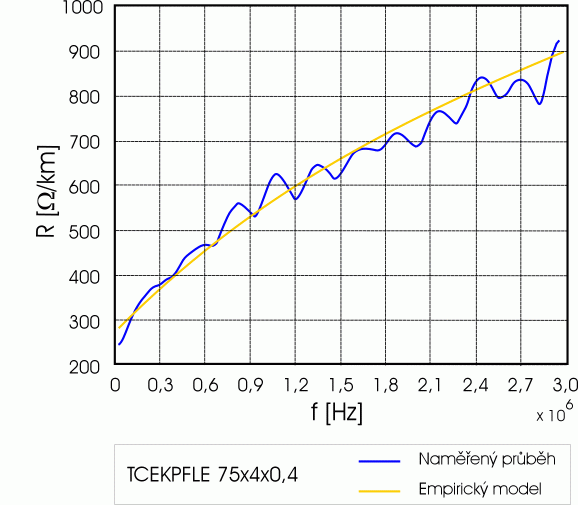
Obr. 5 Porovnání empirického modelu se skutečným průběhem měrného odporu

Obr. 6 Porovnání empirického modelu se skutečným průběhem měrné indukčnosti

Ze simulací provedených v prostředí MatLab vyplývá, že modely pro měrný odpor se liší o méně než 2 % pro d/D ≤ 0,8. Modely pro měrnou indukčnost o méně než 10 % pro d/D ≤ 0,67. Pro měrnou indukčnost jsou modely rozdílné tím méně, čím menší je poměr d/D (čím dále jsou vodiče od sebe).

Závěr

Cílem příspěvku byla ukázka dvou modelů, které mohou být použity pro simulace vedení v přístupových sítích. Význam těchto modelů plyne zejména z faktu, že přístupové sítě jsou dnes stále častěji využívány pro digitální účastnické přípojky xDSL, které jsou provozovány na frekvencích, při nichž se již významně uplatňuje útlum vedení a další negativní vlivy spojené s přenosem.

Tento příspěvek vznikl za podpory grantu NPV 1ET300750402.

Literatura

[1] Hughes, H.: Telecommunications Cables, John Wiley & Sons, West Sussex - England, 1997
[2] Hubený, T.: Symmetric Line Models Based on the Bessel Functions, In Electronics and Telecommunications - Papers. Riga Technical University, Riga, 2005, s. 20-21.
[3] Doporučení ITU-T G.996.1 Test Procedures for Digital Subscriber Line (DSL) Transceivers, 2001
[4] Yoho, J: Physically-Based Realizable Modeling and Network Synthesis of Subscriber Loops Utilized in DSL Technology, Ph.D Thesis, Virginia,2001
[5] Kvasil, J.: Teorie sdělovacích vedení, ČVUT Praha, Praha, 1976