Význam a vlastnosti superkontinua pro telekomunikace

V tomto článku jsou shrnuty základy superkontinua a jeho potenciálního uplatnění v praxi. Jsou zde uvedeny základní rovnice nutné pro popis optického vlnění šířícího se vlnovodem. Pomocí simulací je odvozen optimální tvar pulzu pro generaci superkontinua. Je diskutován vliv parametrů pro generaci superkontinua, přičemž je uvažováno vysoce nelineární vlákno HNLF.

---

Meaning and feature of supercontinua for telecommunication

Abstract

The basic intent of this paper is summary of basis of supercontinua and its potential use in practice. Here are shown basic formulas, which are needed to describe optical wave propagation in optical fiber. With help of simulation optimal shape of pulse for supercontinua generation is derived. Under discussion is parameters' influence for supercontinua generation, whereas highly un-linear fiber HNLF is consider.

---

První práce, která pojednávala o superkontinuu je z roku 1970 [1], [2]. V pokusu z roku 1970 bylo pozorováno spektrální rozšíření při vyšších výkonech laseru. Takovémuto rozšíření spektra, které může dosahovat až několik stovek nm se pak říká superkontinuum. Od té doby se jevy, které způsobují takovéto spektrální rozšíření studovaly důkladně jak z teoretického, tak i praktického hlediska.

Spektrální rozšíření přímo souvisí s koeficientem γ, který charakterizuje vliv nelineárních jevů ve vlákně. Čím větší je γ, tím více se rozšíří spektrum signálu po průchodu vláknem. Vysokého koeficientu γ se dociluje zejména u vysoce nelineárních vláken (Highly Nonlinear Fibers - HNLF) a mikrostrukturních vláken (Photonic Crystal Fibers - PCF). Zatímco u HNLF vláken dosahujeme hodnot γ v řádu desítek W^-1km^-1, u PCF vláken jsme schopni dosáhnout až stovek či dokonce tisíců W^-1km^-1. Protože PCF vlákna jsou velmi drahá, stále se používají pro studium spektrálního rozšiřování HNLF vlákna mající patřičnou délku několika kilometrů. Tak jsme schopni docílit toho, že se nám nelineární efekty postupně nasčítají v délce vlákna a mají stejný efekt jako s použitím několika metrů vláken PCF.

Využití generování superkontinua je velice rozsáhlé a dobře využitelné v praxi. Superkontinuum se dá použít jako optický zdroj pro vlnový multiplex (DWDM), kde potřebujeme několik zdrojů záření pracujících na různých vlnových délkách [3], [4]. Princip je velice jednoduchý. Použijeme zdroj laserový pulzů s optickým zesilovačem. Zesilovač může být jak Ramanovský (RFA), tak i Erbiem dopovaný (EDFA). Signál poté navážeme do HNLF vlákna, které může být dlouhé až několik kilometrů. Na výstupu vlákna již dostáváme rozšířené spektrum. Toto spektrum pomocí optických filtrů rozdělíme na několik nosných, na které je možno namodulovat užitečný signál. Signál může být namodulován ještě před vstupem do HNLF a na výstupu po průchodu optickými filtry dostaneme zkopírovaný signál - docílíme tedy tzv. broadcast. Schéma je vyznačeno na obr. 1.

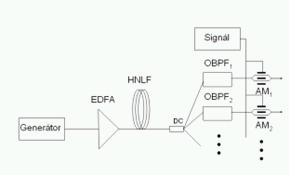
Obr. 1: Schéma optického zdroje DWDM (EDFA - Erbium doped fiber amplifier, HNLF - highly nonlinear fiber, DC - directional coupler, OBPF - optical bandpass filter, AM - amplitude modulator)

Další využití spočívá ve vlnové konverzi [5]. Pomocí přídavného kontinuálního laseru, který prochází vláknem společně se signálem docílíme zkopírování signálu do blízkosti frekvence kontinuálního laseru. Jako další aplikace je možno zmínit optickou koherentní tomografii [6], kde je nutno disponovat zdrojem, který má velmi široké spektrum.

Vlastnosti

Abychom mohli charakterizovat pulzy v nelineárním médiu jako je vlákno s vysokým koeficientem nelinearity, je nutné nejdříve odvodit rovnici, která popisuje šíření pulzů ve vlákně. Taková rovnice - která se nazývá Nelineární Schrodingerova rovnice (NLS) - je odvozena přímo z Maxwellových rovnic. V rovnici

(1)

A(z,t) značí pomalu se měnící obálku, z je vzdálenost, T je normalizovaný čas, α je útlum, β₂ a β₃ jsou první členy Tailorova rozvoje konstanty šíření, j je imaginární jednotka, ω₀ je frekvence, na které pracuje laser a T_R je Ramanovská konstanta. V rovnici (1) jsou lineární jevy probíhající ve vlákně shrnuty na levé straně - jedná se o tlumení pulzu (člen s α), a disperzní jevy (členy s β₂ a β₃). Na pravé straně vystupují nelineární jevy, které jsou všechny úměrné γ. První člen charakterizuje vlastní modulaci fáze, druhý tzv. self-steepening (změna strmosti pulzu) [7] a třetí tzv. self-frequency shift (frekvenční přeliv energie) [7]. Podle [8] je možno dospět k tomu, že nelineární efekty začnou být významné pro vlákna délek.

(2)

kde L_NL je nelineární délka vlákna

(3)

kde P₀ je špičkový výkon generátoru pulzů. Pokud zanedbáme disperzi skupinové rychlosti šíření (GVD), řešení nelineární Schrodingerovi rovnice je

(4)

kde U je normalizovaná amplituda a φ_NL je posun ve fázi. Normalizovaná amplituda je dána

(5)

efektivní délka je definovaná jako

(6)

Maximální fázový posuv je dán rovnicí

(7)

Spektrální rozšíření je dáno rovnicí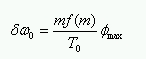

(8)

Pro supergaussovské pulzy, kde m je řád pulzu a f(m) závisí na m pouze málo: pro m=1; f=0.86 a nabývá hodnoty 0.74 pro větší m. Rovnice (8) nám popisuje spektrální rozšíření jako funkci řádu supergaussovského pulzu (v případě řádu 1 dostáváme Gaussovský pulz). V tomto článku jsem se pokusil najít optimální tvar vstupního pulzu tak, aby po průchodu HNLF vláknem jsme dosáhli pokud možno největšího spektrálního rozšíření. Pro testování jsem použil mimo již zmíněných supergaussovských pulzů i obdélníkový a cos². Obdélníkový pulz byl definován v 0.05 násobku jemu vyhrazeného časového intervalu, to samé platilo pro cos² s tím, že faktor roll-off byl 0.5 (velikost náběžné a sestupné hrany). Supergaussovský pulz byl zvolen tak, že jeho FWHM (šířka v polovině maxima) byla 5 ps a byl třetího řádu. Ve všech případech byl použit formát s návratem k nule (RZ). Pro simulaci byl použit předzesilovač s konstantním výstupním výkonem 25 dBm a 5-ti pólový besselovský filtr o šířce pásma 1000 GHz pro pokles 3 dB. Použil jsem vlákno dlouhé 1 km. Jeho parametry jsou shrnuté v tab. 1.

Tab. 1: Vláknové parametry

Obr. 2: Obdélníkový pulz

Obr. 3: Pulz cos²

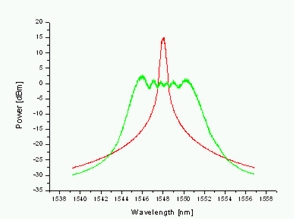
Obr. 4: Gaussovský pulz

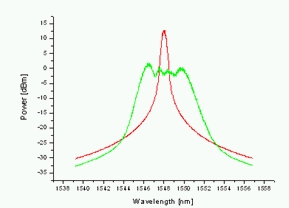
Obr. 5: Supergaussovský pulz třetího řádu

Z obr. 2 až 5 je patrné, že nejlepší výsledky dostaneme při použití Gaussovského pulzu. Spektrální rozšíření je na obr. 4 největší. Toho se pak dá využít např. jako zdroje pro již zmíněný systém DWDM. Výše uvedená pozorování týkající se vlivu tvaru pulzu na spektrální rozšíření berou v úvahu pouze vlastní modulaci fáze (SPM - self-phase modulation). Při vytváření superkontinua se uplatňují i jiné efekty jako je vliv disperze, křížová modulace fáze (XPM - cross-phase modulation), čtyřvlnné směšování (FWM - four-wave mixing) a Ramanův stimulovaný rozptyl (SRS - stimulated Raman scattering).

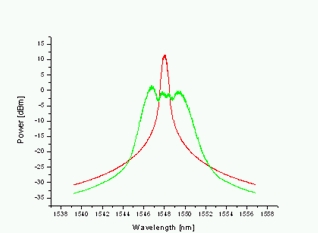
Efekt disperze třetího řádu (TOD) - β₃ je velmi významný pro utváření superkontinua. S většími hodnotami β₃ se rozšířené spektrum stává asymetrickým. Toto může být velmi dobře pozorováno, pokud se nacházíme v blízkosti vlnové délky s nulovou disperzí (ZDW), jinak efekt β₃ je převážen efekty plynoucími z β₂. Výsledky ze simulací, kde ZDW=1560 nm jsou na obr. 6.

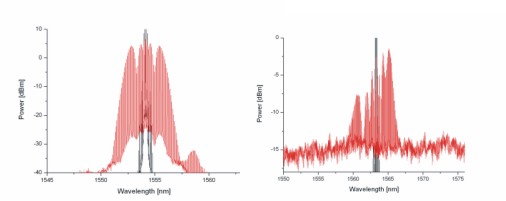
Obr. 6: Vliv β₃, vlevo - daleko od ZDW, vpravo - v blízkosti ZDW

Pokud pustíme do vlákna dva signály a podmínka fázového synchronismu není splněna (β₂ prvního signálu se podstatně liší od β₂ druhého signálu) je možno pozorovat XPM. Tento úkaz je dobře vidět, například když se oba signály šíří v normálním disperzním režimu nebo anomálním disperzním režimu. Pro takovouto konfiguraci potřebujeme dvě svázané NLS rovnice. Fázový posuv vyvolaný dvěma společně se šířícími signály je:

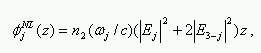
(9)

kde n₂ je nelineární index lomu a E_j je intenzita j-tého signálu. Jak je patrné z rovnice (9), efekty XPM jsou dvakrát silnější než jsou efekty samotného SPM. Simulované výsledky jsou vidět z obr. 7. Oba dva signály se šířily v normálním disperzním režimu (ZDW=1560 nm).

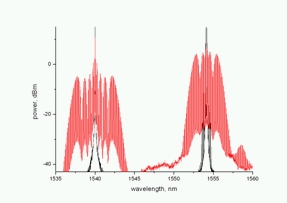
Obr. 7: XPM pro signál na 1554 nm a pumpu na 1540 nm

Pokud počáteční vrcholový výkon sledu pulzů překročí určitý limit aproximovaný rovnicí

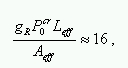
(10)

můžeme pozorovat přenos energie z frekvencí vyšších na nižší. Tento frekvenční posuv je přibližně 13 THz. V rovnici (10) g_R je takzvaný koeficient Ramanovského zisku, P₀^cr je kritický výkon a A_eff je efektivní plocha jádra. Frekvenční posuv 13 THz byl měřen pro sled 1 µm pulzů v křemíkovém vlákně. Koeficient g_R se může významně měnit s příměsemi v křemíkovém vlákně. Nová frekvenční komponenta se nazývá Stokesova vlna.

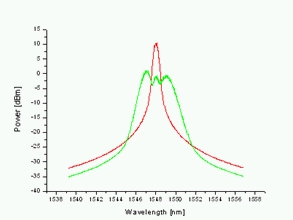
Čtyřvlnné směšování se také uplatňuje v procesu generace superkontinua. Pokud pošleme vláknem dva signály, vzniknou produkty čtyřvlnného směšování na frekvencích 2f₁-f₂ a 2f₂-f₁. Musí být ale splněna podmínka fázového synchronismu a musí být dodán dostatečný výkon. Pro větší výkonové úrovně dostáváme produkty FWM, které se rozprostírají přes větší šířku pásma - obr. 8.

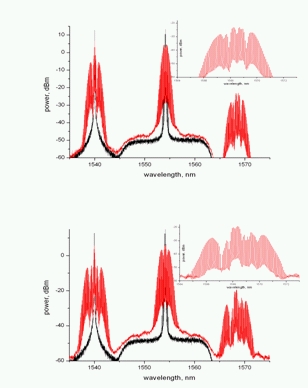
Obr. 8: Porovnání produktů FWM při různých úrovních výkonů: nahoře 20 dBm, dole 22 dBm

Závěr

V tomto článku jsem se snažil shrnout problematiku superkontinua a vlivy jednotlivých parametrů na jeho tvorbu. Nejdříve jsem nastínil použití superkontinua v praxi a poté jsem rozebral některé důležité rovnice. Článek představuje optimální tvar vstupních pulzů tak, aby výsledné spektrální rozšíření bylo co možná největší. Nakonec stručně vysvětluji jednotlivé efekty jak na konkrétních simulacích tak i teoreticky. Některé simulace jsou dostupné zde.

Tento příspěvek vznikl za podpory výzkumného záměru Výzkum perspektivních informačních a komunikačních technologií č. MSM6840770014.

Literatura

[1] Alfano R. R., Shapiro S. L.: Emission in the region 4000 to 7000 A via four photon coupling in Glass, Physical Review Letters, vol.24, p.584, 1970.
[2] Alfano R. R., Shapiro S. L.: Observation of selfphase modulation and small-scale filaments in crystals and glasses, Physical Review Letters, vol.24, p.592, 1970.
[3] Takara H. et al.: Over 1000 channel optical frequency chain generation from a single supercontinuum source with 12.5GHz channel spacing for DWDM and frequency standards, ECOC 2000.
[4] Ohara T. et al.: Over 1000 channel, 6.25 GHz-spaced ultra-DWDM transmission with supercontinuum multi-carrier source, Optical Society of America, 2005.
[5] Sharping J., Fiorentino M., Kumar P., Windeler S.: All optical switching based on cross-phase modulation in microstructure fiber, IEEE Photonics Technology Letters, vol.14, p.73, 2002.
[6] Hartl I. et al.: Ultrahigh-resolution optical coherence tomography using continuum generation in air-silica microstructure optical fiver, Optics Lett., vol.26, 2001.
[7] Trippenbach M., Band Y. B.: Effects of self-steepening and self-frequency shifting on short-pulse splitting in dispersive media, Physical Review Lett, vol. 57, p. 4791, 1998.
[8] Agrawal G. P.: Nonlinear fiber optics: 3rd edition, Academic Press, 2001.