Modelování silnoproudých vedení II – simulace ukázkové sítě
Autor: P. Mlýnek, M. Koutný, J. Mišurec <mlynek(at)feec.vutbr.cz>, Pracoviště: Vysoké učení technické v Brně, Téma: PLC, Vydáno dne: 21. 07. 2010Power Line Modelling II - Simulation of sample network- Abstract
The article is focused on modelling of the sample network distribution topology thanks two methods and assembling of the resulting power line model for data transfer simulation.
Keywords:transfer function, simulation, two-port network, multipath enviroment
Úvod
Počítačová simulace systémů PLC umožní lépe pochopit problematiku přenosů dat po silnoproudém vedení, ukáže možnosti těchto systémů a lépe se vymezí segment použitelnosti PLC. Vytvoření dostatečně přesných počítačových modelů systémů PLC tak výrazným způsobem zefektivní proces výběru a nasazování nových telemetrických a řídicích technologií.
Podle teoretického popisu v prvním příspěvku byly realizovány dva přístupy k modelování silnoproudých vedení. Z odvozených přenosových funkcí bylo silnoproudé vedení modelováno jako filtr určený přenosovou funkcí pro prostředí s vícecestným šířením signálu a také jako kaskádně zapojené dvojbrany. V navržených modelech je kladen důraz na vystižení všech rušivých vlivů, které se mohou vyskytnout na silnoproudém vedení. Vytvoření jednotlivých modelů bylo realizováno v programu Matlab/Simulink [1].
Topologie ukázkové distribuční sítě
Byla uvažována topologie ukázkové silnoproudé distribuční sítě na Obr. 1. Na přenosové cestě mezi vysílačem a příjemce je jedna odbočka. Celá síť je složena ze segmentů (1), (2) a (3) s délkou l1, l2 a l3 a charakteristickou impedancí ZC1, ZC2 a ZC3.

Obr. 1: Topologie ukázkové distribuční sítě
Přenosová funkce prostředí s vícecestným šířením
Pro výpočet přenosové funkce musíme znát hodnoty primárních parametrů vedení R´, L´, C´, G´. Tyto parametry lze získat experimentálním měřením [2] nebo výpočtem [3].
Předpokládáme, že charakteristická impedance všech častí sítě je odlišná a je složena z kabelu CYKY o jiném průřezu. Vysílač a přijímač jsou impedančně přizpůsobené kabelu, na který jsou připojeny, tzn. ZA=ZC1, ZC=ZC2, tudíž zde nedochází k odrazům. Spotřebič na odbočce má jinou impedanci, než kabel, ke kterému je připojen, takže zde bude docházet k odrazům a dále bude docházet k odrazům v místě, kde je odbočka připojena k hlavní větvi.
Výpočtem podle (1)-(4) pro kabely CYKY 3x1.5, CYKY 3x2.5, a CYKY 3x4 získáme primární parametry a na základě těchto parametrů můžeme provést výpočet charakteristických impedancí a měrného činitele přenosu pro každý segment sítě.
 | (1) |
 | (2) |
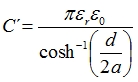 | (3) |
|
| (4) |
Tab. 1: Parametry kabelu CYKY 3x2.5
|
Označení |
Význam |
Rozměr (jednotka) |
|
a |
Poloměr vodiče |
0,892 mm |
|
d |
Vzdálenost mezi středy vodičů |
3,584 mm |
|
σ |
Konduktivita mědi |
58•106 S•m-1 |
|
μ0 |
Permeabilita vzduchu |
4• π• 10-7 H•m-1 |
|
μr |
Relativní magnetická permeabilita mědi |
0,99999 |
|
ε0 |
Permitivita vakua |
8,854•10-12 F•m-1 |
|
εr |
Relativní permitivita izolace |
4 |
Ze známých charakteristických impedancí jednotlivých segmentů ukázkové sítě stanovíme koeficienty odrazů podle rovnic [4] [5]:
 | (5) |
 | (6) |
 | (7) |
Dále je nutné provést výpočet koeficientů přenosu podle rovnic:
|
| (8) |
|
| (9) |
Šíření signálu od vysílače k přijímači může probíhat v odlišných cestách, možné cesty jsou znázorněny v Tab. 2.
Tab. 2: Šíření signálu od vysílače k přijímači pro ukázkovou síť
|
Číslo cesty |
Směr cesty |
Váha cesty gi |
Délka cesty di |
|
1 |
A-B-C |
t1B |
l1+l2 |
|
2 |
A-B-D-B-C |
t1B•r3D•t3D |
l1+2l3+l2 |
|
... |
|||
|
N |
A-B (-D-B)N-1-C |
t1B•r3D• (r3B•r3D)(N-2)•t3D |
l1+2(N-1)l3+l2 |
Každá cesta i má svou váhu gi reprezentující odrazy a faktory přenosu podél cesty. Zpoždění cesty τi lze vypočíst z délky cesty, rychlosti světla ve vakuu c0 a relativní permitivity izolace εr podle rovnice:
 | (10) |
Signál od vysílače k příjemci se může šířit nekonečným počtem cest v závislosti na topologii sítě. Zvětšováním počtu cest N můžeme zvyšovat přesnost modelu. Jelikož útlum vedení A(f,d) roste s délkou a frekvencí, tak s rostoucí délkou cesty je útlum větší a proto je menší váha cesty a tím méně přispívá váha této cesty do celkového signálu na straně příjemce. Z toho důvodu není nutné volit příliš mnoho cest. Pro výpočet bylo zvoleno počet cest N=6.
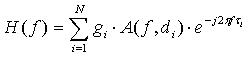 | (11) |
Rovnice (11) reprezentuje přenosovou funkci silnoproudého vedení pro prostředí s vícecestným šířením. Na základě těchto výpočtu byla zjištěna přenosová funkce ukázkové sítě, parametry modelu jsou v Tab. 3 a frekvenční odezva je zobrazena Obr. 2.
Tab. 3: Šíření signálu od vysílače k přijímači pro ukázkovou síť
|
Číslo cesty |
1 |
2 |
3 |
4 |
5 |
6 |
|
di |
200 |
238 |
276 |
314 |
352 |
390 |
|
gi |
0,6664 |
0,2498 |
-0,0408 |
0,0067 |
-0,0011 |
0,0002 |

Obr. 2: Simulace ukázkové sítě pro 6 cest
Přenosová funkce kaskádně zapojených dvojbranuDalší možností modelování silnoproudých vedení je pomocí kaskádních parametrů, které popisují závislost vstupních a výstupních napětí a proudů pomocí dvojbranu. Budeme-li uvažovat ukázkový model na Obr. 1 s jednou odbočkou a tu nahradíme odpovídající impedancí Zeq. Dále budeme uvažovat, že vysílač a přijímač jsou impedančně nepřizpůsobené kabelu, na který jsou připojeny, tudíž zde bude docházet k odrazům a spotřebič na odbočce má impedanci Zbr. Impedanci odbočky vypočteme podle rovnice [6]:
|
| (12) |
kde Zbr a γbr jsou charakteristická impedance a měrný činitel přenosu pro odbočku. Tab. 4 zobrazuje parametry ukázkové distribuční sítě na Obr. 1 a vypočtené hodnoty pro kaskádní zapojení.
Tab. 4:Parametry ukázkové distribuční sítě
|
ZS |
120 Ω |
|
ZL |
600 Ω |
|
Zbr |
300 Ω |
|
Z |
180 Ω |
|
Zeq |
97,67-0,669i Ω |
Obr. 3 a) zobrazuje vedení s jednou odbočkou a na Obr. 3 b) je vedení zjednodušeno.

Obr. 3: a)Vedení s jednou odbočkou. b) Zjednodušené vedení s jednou odbočkou
Na Obr. 3 b) je vedení s jednou odbočkou zobrazeno jako vícenásobné zapojení elementárních dvojbranů, které jsou popsány maticemi A1 až A4:
|
| (13) |
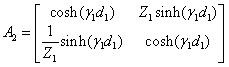 | (14) |
 | (15) |
 | (16) |
kde Z1,γ1, Z2 a γ2 jsou charakteristická impedance a měrný činitel přenosu pro druhý a čtvrtý dvojbran.
Výslednou kaskádní matici modelovaného vedení s jednou odbočkou získáme jako součin dílčích kaskádních matic:
|
| (17) |
kde n je počet dílčích částí popsaných kaskádní maticí. Známe-li parametry ABCD výsledné kaskádní matice, můžeme určit přenosovou funkci pomocí rovnice:
 | (18) |
Na základě tohoto výpočetního aparátu byla zjištěna přenosová funkce ukázkového modelu a frekvenční odezva je zobrazena na Obr. 4. Odrazy v nepřizpůsobené odbočce způsobí periodické zvlnění ve frekvenční odezvě.

Obr. 4: Simulace ukázkové sítě pro impedančně nepřizpůsobený vysílač, přijímač a odbočku
Výsledný kanál modelovaný přenosovou funkcí
Z přenosové funkce prostředí s vícecestným šířením anebo z přenosové funkce dvojbranu byly vypočteny koeficienty FIR filtru a těmito filtry bylo modelováno silnoproudé vedení společně se zdroji rušení. Detailní popis zdrojů rušení a jejich modelů můžeme najít v [7]. Na Obr. 5 je zobrazen výsledný model kanálu modelovaný pomocí přenosové funkce společně se zdroji rušení. Tento model kanálu umožní co nejpřesněji simulovat datovou komunikaci po silnoproudých vedeních.

Obr. 5: Výsledný model kanálu
Závěr
Heterogenní struktura silnoproudé sítě s mnoha odbočkami a impedančními nepřizpůsobeními způsobuje odrazy. Z tohoto důvodu prostředí s vícecestným šířením popisuje typické silnoproudé vedení. Tento přístup modelování vedení se vyznačuje přesností a jednoduchostí. Nevýhodu ve výpočetní náročnosti pro odhad zpoždění, amplitudy a fáze spojené s každou cestou, jelikož je nutné uvažovat s velkým počtem cest.Řešení modelů vedení pomocí kaskádně zapojených elementárních dvojbranů umožňuje relativně jednoduše do modelu vkládat bloky, které umožní modelovat především problémové oblasti této technologie jako je malý dosah užitečného signálu, rušení užitečného signálu na vedení, či vliv jednotlivých prvků energetické sítě, které ovlivňují přenos.
Navržený model umožní na základě simulací provést analýzu konkrétní silnoproudé sítě pro různá specifika přenosového prostředí, tak aby bylo dosaženo co nejlepších parametrů datového přenosu. V budoucí práci je nutné rozšířit navržené modely tak, aby postihovaly všechny rušivé vlivy, které se ve vedení mohou vyskytnout.
Tento příspěvek vznikl za podpory výzkumného záměru Ministerstva školství, č. MSM 0021630513 a grantu FEKT-S-10-16.
Literatura
[1] The MathWorks [online]. 1999 [cit. 2010-05-05]. Online: http://www.mathworks.com
[2] CATALIOTTI, A.; DAIDONE, A.; TINE, G. Power line communications in Medium Voltage system: Characterization of MV cables. IEEE Transactions on Power Delivery, vol. 23, n. 4, 2008.
[3] PAPALEONIDOPOULOS, I.; KARAGIANNOPOULOS, C.; THEODOROU, N.; ANAGNOSTOPOULOS, C.; ANAGNOSTOPOULOS, I. Modelling of indoor low voltage power-line cables in the high frequency range. International Symposium on Power Line Communications and Its Applications (ISPLC).
[4] ZIMMERMANN, M.; DOSTERT, K. A Multi-Path Signal Propagation Model for the Power Line Channel in the High Frequency Range. Proceedings of the 3rd International Symposium on Power-Line Communications, Lancaster, UK, 1999, pp. 45 – 51.
[5] ZIMMERMANN, M; DOSTERT, K. A Multipath Model for the Powerline Channel. IEEE Transactions on Communications. 2002, VOL. 50, NO. 4.
[6] ESMAILIAN, T; KSCHISCHANG, F; GULAK, G. In-building power lines as high-speed communication channels: channel characterization and a test channel ensemble. International Journal of Communication Systems. 2003.
[7] BABIC, M.; HAGENAU, M.; DOSTERT, K.; BAUSCH, J. Theoretical postulation of PLC channel model. Open PLC European Research Alliance (OPERA). 2005