Citlivost metod pro měření podobnosti kvantitativních proměnných

Měření podobnosti analyzovaných objektů je nezbytnou komponentou algoritmů v řadě vědeckých oblastí. V článku jsou popsány nejpoužívanější techniky pro měření podobnosti kvantitativních proměnných a je proveden průzkum vlivu dat reprezentovaných různými intervaly hodnot na tyto metody. Cílem článku je ukázat citlivost použitých metod na měřená data.

---

Sensitivity of Methods for Distance Measurement of Quantitative Variables

Cluster analysis of data plays an important role in many scientific fields, such as: computer sciences, mathematics and statistics, economics, marketing, biology, and medicine. Measuring the similarity of the analyzed objects is an essential component of the algorithms used in cluster analysis. When the appropriate method for measuring the similarity of objects is selected, the nature of the analyzed data should be taken into account. This article describes the most widely used techniques for measuring similarity of quantitative variables and different intervals of values for these methods are taken into account. This article aims to show the sensitivity of the methods used for different data. The result of this survey can help in selecting appropriate methods for measuring similarity of quantitative data.

Keywords: Distance, Measurement, Similarity

---

Úvod

Měření vzdálenosti v podstatě vyjadřuje podobnost resp. odlišnost dvou objektů. Při výpočtu vzdálenosti mezi dvěma objekty hraje důležitou roli, v jakém intervalu hodnot jsou body rozloženy. Výsledná změřená vzdálenost totiž přímo ovlivňuje výsledné shluky dat - jejich strukturu, která se tak pokaždé může lišit. V závislosti na tom, jakých hodnot nabývají příznaky popisující měřené objekty, volíme metodu měření vzdálenosti. Lze předpokládat, že vzdálenost mezi objekty v rámci jednoho shluku bude minimální a naopak vzdálenost mezi objekty různých shluků bude maximální.

Pokud dokážeme podobnost resp. odlišnost měřit, budeme schopni rozlišit jeden objekt od druhého. Na základě tohoto měření může být dále prováděna např. již zmiňovaná shluková analýza dat. Hlavním cílem tohoto článku je provést průzkum metod měřících vzdálenost mezi kvantitativně vyjádřenými příznaky popisující objekt. Na základě tohoto průzkumu provést srovnání citlivosti jednotlivých metod na data z různých intervalů hodnot a pomoci při výběru vhodné metody měření vzdálenosti třeba právě při shlukové analýze dat, což je hlavním přínosem a motivací pro vytvoření tohoto článku. Na základě vhodně provedené shlukové analýzy je možné lépe porozumět charakteristice zkoumaných dat, vysvětlit jejich chování, klasifikovat objekty do skupin či dokonce predikovat chování nových objektů.Tento článek byl inspirován shlukovou analýzou obrazových dat v rámci projektu Ministerstva průmyslu a obchodu ČR, č. FR-TI4/151, kde byly jako jednotlivé souřadnice brány RGB hodnoty zkoumaného bodu, avšak pro samostatná měření uvedená v sekci 3 byla použita syntetická data, aby byla lépe vidět výhoda použitých metod na různě připravená data

Měření podobnosti objektů je velice rozsáhlá problematika, o čemž svědčí publikace [1], kde je uvedeno nepřeberné množství metod pro měření vzdálenosti používaných v nejrůznějších oborech. Obecně rozlišujeme čtyři základní kategorie proměnných – binární, nominální/kategorické, ordinální a kvantitativní. Více o těchto typech proměnných a měření jejich podobnosti lze najít např. v [1], [2]. Tento článek se blíže zaměřuje na metody pro měření vzdálenosti mezi objekty popsanými kvantitativními proměnnými a jejich citlivostí na data reprezentovanými hodnotami z různých rozsahů hodnot. Jakýkoliv objekt je v tomto případě reprezentován n příznaky, které jej popisují. V medicínské praxi je tedy např. objektem pacient. Tento pacient je popsán několika příznaky, jako je např. výška, váha a další příznaky vypovídající o stavu pacienta. Každý objekt je potom vyjádřen vektorem hodnot těchto n příznaků, které reprezentují souřadnice objektu v n-rozměrném prostoru.

Problematika měření podobnosti ovlivňující shlukovou analýzu dat byla již zkoumána např. v [4], kde byl proveden výzkum vlivu měření vzdálenosti na různé shlukovací algoritmy. Pro tyto účely byla vytvořena množina syntetických dat a množina reálných dat z prostředí kriketu, na kterých bylo testování provedeno. V článku [4] byly testování podrobeny tyto vzdálenostní funkce: Euklidovská vzdálenost, Bit-Vector vzdálenost a Komparativní vzdálenost. Dále byla problematika vzdálenosti zkoumána v [3], kde byla přímo zkoumána vhodnost použití jednotlivých technik pro různé shlukovací algoritmy. Oba dva zdroje srovnávají různé funkce a každá z trochu jiného pohledu, navíc se v těchto článcích míchají binární a kvantitativní proměnné. Trochu jiným přístupem se zabývá článek [5], který se snaží naučit vhodnou metodu porovnávání vzdálenosti podle již provedené shlukové analýzy. V našem článku se zaměřujeme striktně na kvantitativní proměnné a snažíme se poskytnout přehled citlivosti šesti nejpoužívanějších měřících metod.

Podobnost (similarity) objektů vyjadřuje kvantitu, která reflektuje sílu vztahu mezi dvěma objekty resp. dvěma příznaky. Tato kvantita se obvykle vyjadřuje v rozsahu hodnot od -1 do +1 nebo v normalizované formě od 0 do +1. Podobnost mezi příznakem i a příznakem j je vyjadřována jako s_ij.

Vzdálenost (distance) objektů d_ij v podstatě určuje odlišnost (dissimilarity) objektů. Měření vzdálenosti je založeno na základě měření neshody příznaků popisujících objekty. Pokud hovoříme o vzdálenosti, můžeme se také setkat s pojmem metrika, a to v případě, pokud jsou splněny všechny čtyři podmínky definující vzdálenost. Jelikož ne všechny techniky měření vzdálenosti splňují čtvrtou podmínku, nejsou všechny vzdálenosti metrikami, ale na druhou stranu, všechny metriky jsou vzdálenostmi.

Definice vzdálenosti:
• d_ij >= 0 (vzdálenost je vždy kladná nebo nula)
• d_ij = 0 (vzdálenost je nula jen když měříme jeden prvek k sobě samému)
• d_ij = d_ji (vzdálenost je symetrická)
• d_ij <= d_ik + d_jk (vzdálenost splňuje trojúhelníkovou nerovnost)

Normalizujme-li odlišnost objektu i od objektu j jako δ_ij, vztah mezi podobností a odlišností bude dán vztahem s_ij = 1 - δ_ij. Pokud hodnota podobnosti není normalizována a leží v intervalu -1 do +1 a odlišnost je měřena v intervalu od 0 do +1, je vzájemný vztah dán rovnicí s_ij = 1 - 2δ_ij.

Článkek je do sekcí rozdělen následovně. Druhá sekce se zabývá metodami pro měření kvantitativních proměnných, v čele s nejznámější metodou, kterou je euklidovská vzdálenost. Jsou zde popsány nejpoužívanější metody pro výpočet vzdálenosti, je uveden vzorec pro jejich výpočet a nejběžnější aplikace. Třetí sekce popisuje měření citlivosti metod vůči hodnotám z různých intervalů. V závěru článku jsou shrnuty dosažené výsledky.

Měření vzdálenosti kvantitativních proměnných

Pro měření vzdálenosti mezi objekty bylo navrženo množství metod. Tyto metody je možné nalézt v [1], kde se s nimi také čtenář může blíže seznámit. Nejčastěji používané techniky jsou uvedeny v dalším textu s krátkým popisem, vzorcem a nejčastější aplikací. V následujících vzorcích je použito toto označování proměnných: d_ij … vzdálenost (odlišnost) bodu i od bodu j, s_ij … podobnost bodu i a bodu j, n … počet příznaků popisujících objekt, x_ik … k-tý příznak objektu i, x_jk … k-tý příznak objektu j, w_k … váha příznaku k, λ … speciální parametr Minkwského vzdálenosti.

Euklidovská vzdálenost (Euclidean distance) je nejvíce používanou metodou pro měření vzdálenosti kvantitativních proměnných. Představuje měření vzdálenosti dvou bodů tak, jako by byla změřena pravítkem – jde tedy o přímou vzdálenost mezi dvěma body (1). Ve většině případů, když je myšleno měření vzdálenosti, půjde s největší pravděpodobností právě o Euklidovskou vzdálenost. Tato vzdálenost je určena jako druhá odmocnina sumy čtvercových vzdáleností mezi souřadnicemi objektů. Euklidovská vzdálenost je speciálním případem Minkowského vzdálenosti s parametrem λ = 2. Je vždy větší nebo rovna nule (pro identické body), vyšší hodnoty vychází pro body vykazující menší podobnost. Existuje také několik druhů této metody, např. Čtvercová Euklidovská vzdálenost (2), Poloviční čtvercová Euklidovská vzdálenost nebo Vážená Euklidovská vzdálenost (3). Např. Čtvercová Euklidovská využívá v podstatě stejného principu jako běžná Euklidovská vzdálenost – ovšem bez odmocniny, a pokud je využita v Jarvis-Patrickově nebo K-means shlukovacím algoritmu, na výsledku se změna neprojeví a má tak příznivý účinek na rychlost výpočtu. Tato změna ovšem negativně ovlivňuje hierarchické shlukovací algoritmy. Aplikovat ji lze na různá intervalová data, používá se i v oblasti psychologie a analýzy DNA, nefunguje dobře pro zpracování obrazových dat a klasifikaci dokumentů, protože výsledky jsou silně ovlivněny příznaky, které mají vysokou hodnotu. Výpočet je dán vzorci:

(1), (2), (3)

Manhattanská vzdálenost (Manhattan distance, City Block distance, Boxcar distance, Rectilinear distance, Absolute Value distance) reprezentuje vzdálenost mezi dvěma body, které si lze představit jako křižovatky v silniční síti městské zástavby. Jde o vzdálenost vyjádřenou jako sumu horizontálních a vertikálních cest z bodu A do bodu B (jako by se šlo po ulicích kolem budov a není možné jít přímo, diagonálně). Tato vzdálenost je speciálním případem Minkowského vzdálenosti s parametrem λ = 1. Je vždy větší nebo rovna nule (pro identické body) a vyšší pro body vykazující menší podobnost. Využívá se hojně v integrovaných obvodech, kde jsou vodiče vedeny paralelně k ose X nebo Y, nefunguje příliš dobře pro zpracování obrazových dat a klasifikace dokumentů. Vzdálenost se vypočítá podle vzorce:

(4)

Čebyševova vzdálenost (Maximum Value distance) prozkoumává absolutní velikost odlišností mezi souřadnicemi dvou objektů. Tato vzdálenost může být použita pro ordinální i kvantitativní proměnné. Jde o speciální případ Minkowského vzdálenosti s parametrem λ = ∞. Tato vzdálenost je výhodná pro objekty, jejichž odlišnost se posuzuje spíše podle individuálních parametrů než podle všech parametrů objektu jako celku. Vzdálenost se vypočítá podle vzorce:

(5)

Minkowského vzdálenost je obecnou metrikou pro měření vzdálenosti. Souvztažnost s jinými typy vzdáleností (hodnota parametru lambda) byla zmíněna v jednotlivých odstavcích výše. Vzdálenost se hodí pro měření jak ordinálních, tak kvantitativních proměnných a vypočítá se podle vzorce:

(6)

Canberrova vzdálenost jedná se o metriku, která je definována jako absolutní hodnota vzdálenosti mezi proměnnými dvou objektů podělená sumou absolutních hodnot těchto proměnných. Každý výsledek tohoto podílu odlišnosti zlomku má hodnotu mezi 0 a +1. Tato vzdálenost sama o sobě ovšem hodnotu mezi 0 a +1 mít nemusí. Je používána, pokud jsou měřené body v blízkosti jejich vzniku a je velmi citlivá pro hodnoty blížící se nule. Tato vzdálenost je velmi citlivá na malé změny pokud se obě souřadnice nachází blízko nule. Její výpočet se provede podle vzorce:

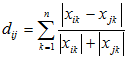(7)

Bray-Curtisova vzdálenost (Sorensenova vzdálenost, Czekanowski’s coefficient) je normalizovanou metodou používanou často v botanice, ekologii a environmentálních vědách. Nahlíží na problém podobně jako Manhattanská vzdálenost (mřížka představující silniční síť v městské zástavbě). Vzdálenost má tu dobrou vlastnost, že pokud jsou všechny souřadnice pozitivní, jejich hodnoty jsou mezi nulou a jedničkou. Normalizace je provedena použitím absolutní odlišnosti dělené sumou součtu hodnot proměnných. Výpočet této vzdálenosti je dán vzorcem:

(8)

Měření citlivosti metod pro měření vzdálenosti

V rámci zkoumání citlivosti metod pro měření vzdálenosti mezi dvěma body bylo provedeno dvanáct měření. Během prvních tří měření byla zkoumána citlivost metod při měření vzdálenosti hodnot blížícím se nule. Souřadnice bodu A byly nastaveny a hodnoty (0,001;0,001) a bodu B na hodnoty (0,01;0,01). Změřené vzdálenosti pro tyto body jsou zaneseny v tabulce 1 jako „Měření 1“. Při druhém měření byla provedena změna souřadnic bodu A na (0,002;0,001) a opět byla změřena vzdálenost bodu A a bodu B. U třetího měření byl bod A nastaven na souřadnice (-0,001;0,001). Ve všech tabulkách se vyskytují měření těmito metodami: Euklidovská vzdálenost, Manhattanská vzdálenost, Čebyševova vzdálenost, Minkowského vzdálenost s parametrem λ = 3, Canberrova vzdálenost a Bray-Curtisova vzdálenost. V každé tabulce je také vidět absolutní rozdíl a relativní odchylka mezi první a druhým měřením (v rámci tabulky) a první a třetím měřením (v rámci tabulky), z čehož je možné usoudit, která metoda bude pro požadované měření vzdálenosti výhodnější.

Tabulka 1 : Měření vzdálenosti dvou bodů blížících se nule.

	Měření 1	Měření 2	Absolutní rozdíl měření 1 a měření 2	Relativní odchylka měření 1 a měření 2	Měření 3	Absolutní rozdíl měření 1 a měření 3	Relativní odchylka měření 1 a měření 3
	A1=0,001 A2=0,001	A1=0,002 A2=0,001			A1=-0,001 A2=0,001
	B1=0,01 B2=0,01	B1=0,01 B2=0,01			B1=0,01 B2=0,01
Euclidean	0,0127	0,0120	0,0007	2,83%	0,0142	0,0015	5,58%
Manhattan	0,0180	0,0170	0,0010	2,86%	0,0200	0,0020	5,26%
Čebyšev	0,0090	0,0090	0	0,00%	0,0110	0,0020	10,00%
Minkowski	0,0113	0,0107	0,0006	2,73%	0,0127	0,0014	5,83%
Canberra	1,6363	1,4848	0,1515	4,85%	1,8181	0,1818	5,26%
Bray-Curtis	0,8181	0,7391	0,0790	5,07%	1,0000	0,1819	10,00%

V dalších třech měřeních byla měřena citlivost metod pro měření vzdálenosti mezi dvěma body, kdy body dosahují relativně vysokých hodnot (vzdálených od nuly). V měření 4 byly souřadnice bodu A nastaveny na hodnoty (1000;1000) a souřadnice bodu B na hodnoty (100; 100). Bylo provedeno měření těchto zadaných bodů, při dalším měření byl změněn bod A na souřadnice (1002;1000) a vypočítána jeho vzdálenost k původnímu bodu B. U šestého měření byl bod A změněn na souřadnice (-1000;1000) a vypočítána vzdálenost opět k původnímu bodu B. V tabulce 2 jsou uvedeny vypočítané hodnoty vzdálenosti pro tyto další tři měření.

Tabulka 2 : Měření vzdálenosti dvou bodů vzdálenějších od nuly.

V předposledních třech měřeních byl použit jeden bod se souřadnicemi od nuly vzdálenějšími A = (1000;1000) a jeden bod velmi blízko nule B = (0,001;0,001). Výsledky měření vzdálenosti těchto dvou bodů jsou uvedeny v tabulce. Při sedmémměření byly změřeny vzdálenosti originálních bodů A a B. Při osmém měření byl bod A lehce posunut na souřadnice A = (1002;1000) a opět změřena vzdálenost k bodu B. V devátém měření byly souřadnice bodu A nastaveny na souřadnice (-1000;1000) a změřena vzdálenost k původnímu bodu B.

Tabulka 3 : Měření vzdálenosti bodu blížícího se nule a bodu vzdálenějšího od nuly.

V posledních třech měřeních je demonstrováno rozložení bodu, kdy vždy jeden z bodů má jednu souřadnici blížící se nule a jednu rapidně vzdálenější. Pří těchto měřeních se ukázalo, že téměř všechny použité metody dosahují stejných neb o velice podobných výsledků. Pro desáté měření byl bod A nastaven na souřadnice (0,01;1000) a bod B na souřadnice (0,001;1000). V jedenáctém měření byl bod A posunut na souřadnice (0,01;1002) a bod B zůstal zachován. V posledním, dvanáctém měření byl bod A posunut na souřadnice (-0,01;1000) a bod B zůstal opět zachován. Výsledky jsou zaneseny v tabulce 4.

Tabulka 4 : Měření vzdálenosti bodů, kde se jedna souřadnice blíží nule a druhá je výrazně vyšší.

Vyhodnocení citlivosti metod pro měření vzdálenosti

K vyhodnocování citlivosti metod měřících vzdálenost mezi objekty můžeme přistupovat ze dvou hledisek. První hledisko dává důraz na odlišení objektů za každou cenu, i když mají velmi podobné hodnoty příznaků (souřadnice). Mezi velmi podobnými hodnotami některé z metod již rozdíl nerozlišují, tedy některé metody nemají dostatečnou rozlišovací schopnost, aby byl rozdíl vidět na první pohled (zde může jít například o číslicové vyjádření na určitý počet desetinných míst) a byť jde o rozdílné souřadnice dvou objektů, jsou tyto objekty reprezentovány jako jeden identický objekt. V případě, že má být rozlišovací schopnost maximální, je vhodné zvolit takovou metodu, která má mezi podobnými hodnotami příznaků dvou objektů takové výsledky, jejichž rozdíl je větší než u jiných metod s rozlišovací schopností na velký počet desetinných míst.

Druhým přístupem je nahlížení na problematiku metod měřících vzdálenost mezi objekty z hlediska šumu. Tento přístup je přesným opakem předchozího. V podstatě jde o to, aby byla zvolena taková měřící metoda, která rozlišuje objekty, až od určité vzdálenosti tzn., že se dokáže vyrovnat se šumem, který mohl mírně změnit hodnoty příznaků (souřadnice) objektu, ale jedná se pořád o tentýž objekt, pouze posunutý o určitou minimální vzdálenost. Na základě těchto dvou přístupů, lze jednoduše vybrat, jakou měřící metodu budeme v projektu používat. V případě, že má být rozlišovací schopnost metod odolná vůči informačnímu šumu a hodnoty příznaků jednoho objektu mohou být posunuty, je třeba zvolit metodu s odpovídající rozlišovací schopností, která rozlišuje objekty až od určité vzdálenosti.

Dále byl také do všech tabulek přidán výsledek výpočtu, který znázorňuje relativní odchylku vždy mezi první a druhým měřením v rámci tabulky a mezi prvním a třetím měřením v rámci tabulky. Tato relativní odchylka ovšem nemusí být vždy jednoznačně vypovídající o výsledku, jelikož z ní není patrná citlivost metod – tedy, na kolik desetinných míst je výsledek vyjádřen, a i když je relativní odchylka vysoká (nyní bereme v potaz maximální rozlišovací schopnost metody v tabulce 1, metoda Čebyšev), nemusí být metoda nejlepší, jelikož nebere v potaz desetinná místa. Na základě tohoto zjištění doporučujeme posuzovat výsledek ne jen podle relativní odchylky, ale i podle absolutního rozdílu daných měření, který znázorňuje požadovanou citlivost na měřená data.

Obecně lze říci, že využití Euklidovské vzdálenosti nebo Čtvercové Euklidovské vzdálenosti je použitelné ve všech případech, i když se nejedná o ideální přístup. Rozlišovací schopnost této měřící metody čítá desetinná místa a je schopna měřit nejen vzdálenosti blízké či vzdálené od nuly, ale i jejich kombinace. Tuto metodu si stanovíme jako referenční a budeme její výsledky porovnávat s výsledky ostatních testovaných metod.

Pokud měříme hodnoty blížící se nule (viz tabulka 1), je jednoznačně nejlepší a nejpřesnější volbou měřit vzdálenost pomocí Canberrovy vzdálenosti. Pomocí této vzdálenosti lze změřit i velmi malé rozdíly mezi objekty. S podobnou přesnosti u takto malých hodnot pracuje i Bray-Curtisova vzdálenost. Pokud se budeme dívat na problém měření hodnot blížících se nule z druhé strany, tedy metody musí vykazovat jistou odolnost vůči šumu, je vhodné použít např. metodu Čebyševovy vzdálenosti, která malé rozdíly při měření vzdálenosti nereflektuje.

V případě měření hodnot vzdálenějších od nuly – viz tabulka 2, vychází měření v případě citlivosti příznivě pro Minkowského metriku a Euklidovskou vzdálenost, která mají velmi dobrou rozlišovací schopnost právě pro hodnoty vzdálenější od nuly. Naopak, při takto zadaných hodnotách selhává právě Canberrova a Bray-Curtisova vzdálenost, které pro výsledné hodnoty nevykazují téměř žádnou vzdálenost. Stejný případ je měření vzdálenosti bodu vzdálenějšího od nuly a bodu blízkého nule - viz tabulka 3, kdy se osvědčilo měření vzdálenosti pomocí Euklidovské vzdálenosti a Minkowského metriky a selhání Canberrovy a Bray-Curtisovy vzdálenosti. V posledních třech měřeních je demonstrováno rozložení bodu, kdy vždy jeden z bodů má jednu souřadnici blížící se nule a jednu rapidně vzdálenější – viz tabulka 4. Z naměřených výsledku je vidět, že metody dosahují téměř stejných nebo podobných výsledků, až na metody měření Canberrovy a Bray-Curtisovy vzdálenosti, které jsou vhodnější pro měření bodů blízkých nule. Na základě těchto výsledků lze pro měření doporučit obecnou a známou Euklidovskou vzdálenost.

Závěr

Tento článek zkoumá existující metody pro měření vzdálenosti mezi objekty využívané např. v algoritmech pro shlukovou analýzu dat. Článek se konkrétně zabývá zkoumáním citlivosti metod na analyzovaná data a jeho výstupem je srovnání těchto metod a doporučení, v jakém případě by měla být která metoda použita. Toto srovnání pomůže dalším výzkumníkům v dané oblasti při rychlém rozhodování, kterou metodu pro měření vzdálenosti v dané situaci použít. Pro měření vzdáleností bodů se souřadnicemi blížícími se nule je vhodné využít Canberrovu nebo Bray-Curtisovu vzdálenost. Pro hodnoty vzdálenější od nuly a hodnoty nejrůznějšího charakteru je vhodné použít Minkowského metriku s parametrem ?=3 a Euklidovskou vzdálenost.

Vznik článku byl podpořen výzkumným projektem Ministerstva průmyslu a obchodu ČR, č. FR-TI4/151 a interním grantem Fakulty elektrotechniky a komunikačních technologií Vysokého učení technického, evidenční č. FEKT-S-11-17.

Literatura

[1] Deza, M. M.; Deza E.; Encyclopedia of Distances. Springer-Verlang Berlin Heidelberg, 2009, s. 583, [online] Dostupné z www: http://www.uco.es/users/ma1fegan/Comunes/asignaturas/vision/ Encyclopedia-of-distances-2009.pdf
[2] Kardi, T.; Similarity Measurement. 2006. [online] Dostupné z www: http://people.revoledu.com/kardi/tutorial/Similarity/
[3] Pandit, S., Gupta, S.; A comparative study on distance measuring approaches for clustering, International Journal of Research in Computer Science, vol. 2, issue 1, s. 29-31, 2011, ISSN 2246-8265
[4] Vimal, A.; Valluri, S. R.; Karlapalem, K.; An Experiment with Distance Measures for Clustering, Technical Report: IIIT/TR/2008/132, 2008. [online] Dostupné z www: http://www.cse.iitb.ac.in/~comad/2008/PDFs/61-ankita.pdf
[5] Bar-Hilel, A., Hertz, T., Shental, N., Weinshall, D.; Learning distance functions using equivalence, Proceedings of the Twentieth International Conference on Machine Learning (ICML-2003), Washington DC, 2003.