Network Tomography Overview and Botnet Network Estimation, Part I.
Autor: V. Oujezský, V. Škorpil, M. Jurčík <vaclav.oujezsky(at)phd.feec.vutbr.cz>, Pracoviště: Vysoké učení technické v Brně, Téma: Aplikace, sítě a služby, Vydáno dne: 23. 06. 2015Abstract: The control of network availability uses a lot of technical methods to provide an overview about the security and quality of services. This article discusses about network tomography technology and intention to use such methods in combination with other techniques to estimate the appearance of a botnet network. This paper’s concept presents a shortened first part of research writing and proposes and brings an idea. The second part with practical tests will follow.
Keywords: botnet; genetics; measurement; network tomography; optimization.
INTRODUCTION
Network behavior and adaptability to a demanded data transfer is under the focus of institutions which provide connectivity, security and also services to maintain almost 99,99% network usability. As the Internet of Everything (IoE), Internet of Things (IoT), Software Defined Network (SDN), other sophisticated platforms, protocols and, of course new cyber security laws are coming, the field of Network Tomography (NT) is growing. In addition, the computing power of equipment continues to increase, along with the development of new storage devices. The first significant mention of Network Tomography was in 1996. This term was used by Vardi [1]. His intention was to capture the relationship between origin destination matrix (OD) estimation through link counts II-A.This article has also been inspired by examples and on-line tools; such as The Center for Applied Internet Data Analysis (CAIDA) [2], which collects a lot of tools provided by researchers or RIPE Labs [3]; to analyze which techniques and algorithms are mostly used to recognize a network flow, bottlenecks etc. Generally, all of them use passive or active access to measure, parse and evaluate data flow. Modern techniques add methods such as Symbolic Regression, Bayesian Networks, SVN and Gene Algorithms. OD estimation uses techniques as are Gaussian Model, Maximum Likelihood Estimation (MLE), Iterative Proportional Fitting (IPF), Maximum Pseudo-Likelihood Estimation (MPLE) or Partial Measurement (PM).
NETWORK TOMOGRAPHY OVERVIEW
Network Tomography is a discipline that studies the internal behavior and characteristics of a network by external sources. These sources include endpoints, edge nodes and network probes, computers, mobiles, routers and other specialized equipment. All of these can provide data to use for analysis. For an example, an illustration of a network is shown in Fig. 1. The blue nodes cooperate and can provide some data to analyze it. The red nodes cannot be set up to estimate some data for various reason. NT proclaims that it is possible to effectively map the data path, capacity, quality, attacks, outward and so on by using this data information, if they are passively stored or actively real-time examined. For example, when generating certain selected probe traffic. We can say that these endpoints are kind of traffic monitors. What the proper monitors are able to do and what they are able to implement is another question. The basic classes of NT can be considered as loss and delay tomography. The extended classes are behavior, typification, matrices representation.
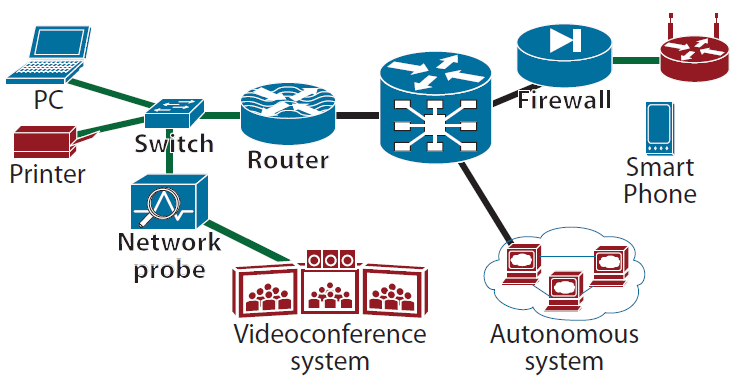
Fig. 1: Network Ilustration.
A. Graph Theorem in Network TomographyThe bases of the NT theorem is given by the widely knowing graph theorem. Let graph Gi = (ν, ε), where the nodes ν represent equipment, with vertex set ν = {1, 2, 3,...|ν|} and ε represent the links among those equipment, edge from set ε ⊆ ν × ν. Then, (ν,ν') ∈ ε denotes a directed edge PG and δG(ν,ν') the shortest edge PδG from ν to ν'. Let be assumed connected graph, not incoherent. The graph, as is shown in Fig. 2, contain one edge for each node to node communication and one vertex for each node.
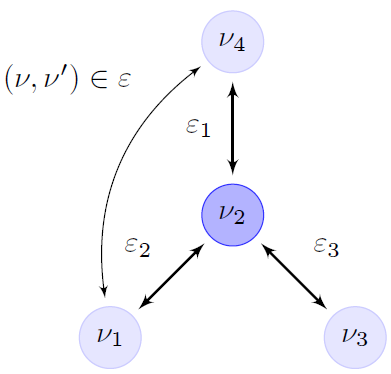
Fig. 2: NT graph representation.
For example, let multicast delay estimation, when a tested frame is sent from node ν4 to node ν1 and ν3, where the delay is observed at the receivers only,the problem to infer the distribution of the internal links delay ε1, ε2, ε3 be as is shown in Equation (1),
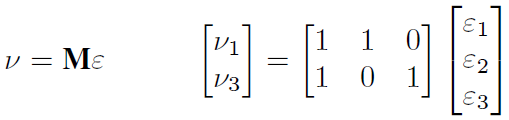 |
(1) |
where numbers 1 in matrix M express the path of probes.
MULTI-OBJECTIVE OPTIMIZATION QUICK OVERVIEW
Multi-Objective Optimization (MOO) given the multiple fitness function (objectives) or goals, is able to find optimal solutions with respect to all criteria simultaneously, as discussed by Riccardo Poli et al. [4], for example. This article describes many examples of MOO usage. Generally, optimization operated such that if a problem is optimized, finds a set of decision variables. Those variables satisfied constraints and a vector function is optimized simultaneously. Such vector, which include elements, express the objective function of all decision and it leads to a non unique solution.
DISCUSSION OF INTENT AND PROBLEM
Our aim is to use the knowledge of network tomography, in combination with multi-objective optimization in order to detect the appearance of a botnet network. We are doing this in such a context that after knowing this type of network it would be possible to isolate the reproductive behavior of a botnet code into small areas, without the possibility of further spread1. It means that the network probes will be used in real time as the monitors of patterns, and based on the NT identification and prediction of a botnet network would to isolation operation such blockage on predicted network elements.
1The two basic types of botnet network exists. Centralized and peer-to-peer (P2P) botnet. As is the first type more controllable, the second is not. The first is created by a root and spreads or connect contested node by a tree connection. The second type creates a mash topology, it means, it doesn’t use a centralized root-server. Every node in P2P can act as a root. From such point of view it is a lot harder to stop this kind of botnet.
A. Proposed intention of use the graph theory
Be graph theory adopted by NT and used in its simple form. For our intention let lists Y = {y(1), ..., y(N)}, where N = {G1, G2, ..., Gi | Gi ≈ Gi+1} and y(n) = {y1(n), ..., y|ν|(n)} associated with the coefficients ai = {0, 1}|ν| . Let for first use, N = {G1, G2 | G1 ≈ G2} ∈ ai then, the element yi(g1) is the occurrence of a node i∈PG1 and yi(g2) will express demanded attributes of G1. Generally, NT aims to infer certain properties on ε of the total value found on node list y|ν|. NT approach can observe the occurring probability of data pattern clusters, if be observed on the node ν|ε| data pattern presence D. And because it is a location problem, it leads to a combinatorial problem. And as such, it is NP-hard problem and requires heuristics to solve. We strive to test it with the multi-objective optimization to infer clusters probability of D from discussed Y. We take over the idea presented by GEN et. al. [5], where authors discussed the whole problematic of network model and optimization. Minarik et. al. [6] discuss about set of weight rules. Further, we simplify it on our intention.
B. Summary steps
To start with, we used knowing node ν as a origin of the
outgoing flow to the rest of the network. In the figure 3 this
node is expressed by the label “source”. Also the appearance
of the network is known. (It is possible for an internet-service
provider (ISP) to have such overview), then;
- set adjacency matrix of network (ISPs know it),
- set the incidence matrix of botnet occurrence in the
proper time t(founded by available probes),
- set sub-weights for ε by:
- observed total ingress flow in the proper time t on
a node ν(captured by an existing probe),
- observed total flow in the proper time t − 1, as
is in a) (“This value is arguable and for further
discus, due to implemented tests and results, what
can be used as a reference flow or how to set the
best weight for an entire mash”),
- repeat the same steps for the outgoes flow, as is
in b),
- determine the difference between t and t − 1 and use determined values by NT as is discussed in IV-A; which is followed:
Rashida A. Memon et. al. wrote their article [7] about network tomography using genetic algorithms and they present methods to estimate the links metric vector by minimizing generalized least-squares problem. We use this idea to recompute observed superfluous flow discussed by proposed summary above, to divide it to partial ε by NT. This values on the each path are used as a sub-weight as stated.
- observed total ingress flow in the proper time t on
a node ν(captured by an existing probe),
- solve second sub-weights as a probability of occurrence D,
- set constraints,
- use multi-objective algorithm to solve maximum spanning tree
“(It can be simply done by solving minimum spanning tree with the recursive values)”
and minimum function of least-square flow with mutual respect,
- use solved resultant vector path by recursive NT interpretation
to select the best divider of botnet network,
Follow the steps declared in summary section;
1) Adjacency matrix: Let a directed graph N, Fig. 3, which
shows a very simple network created by nodes (subgraph G).
Lines which connect the nodes simply represent a provider
network which can detect a botnet pattern. Then, the blue
nodes represent the contested node. Y list express |ν| lists Y =
{y1, yi, ..., y|ν|} for yi
contains all nodes j where subgraph G include an i∼j.
For simple graph N, Fig. 3, we can represent
lists as follows: Y lists y1 = {2, 3}, y2 = {4, 5},
y3 = {2, 5, 6}, y4 = {6, 7}, y5 = {4, 6, 7},
y6 = {7}, y7 = {:}
and Y adjacency matrix of lists is shown in Equation (2).
Matrices are not ideal for practical purposes, but are very good
for theoretical use to solve a network problem. Thanks to this
obviousness we realize calculations with such representation.
 |
(2) |
2) Incidence matrix: incidence matrix D is composed in the same way. It express relation R as the D estimation as is shown in Equation (3). We end up with two matrices. The matrix of lists adjacency and occur.
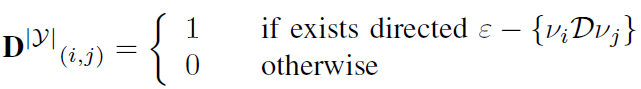 |
(3) |
3) Flow sub-weights: let computed flow 𝔽, for our theoretical purpose predefined. To compute proper set of 𝔽̂ε consider Equation (4):
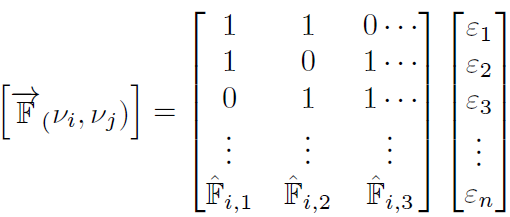 |
(4) |
Matrix in Equation (4) is the opposite of an adjacency matrix,
because it monitors the quantity of incoming traffic to a node
(vector) not an outgoing traffic and is predicted that a Botnet
network will generate some overhead traffic from each node.
Each node in a P2P Botnet network is both a server and
endpoint. It is possible to compute flows as an increasing flow
in each transfer point. Practically, it is expected that we will
know only 𝔽 which comes from “some source” to the each
endpoint.
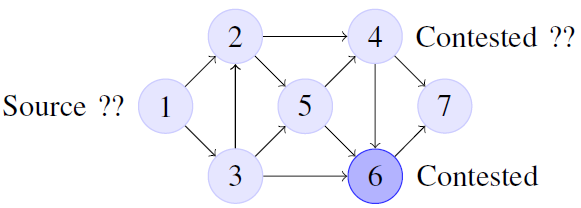
Fig. 3: Graph N.
- We can use in this case the above calculation NT to solve each
𝔽̂ ⇒ matrix N. It means, that the functional
values of the function f are known only at discrete set
of points works with scalar product of elements. Therefore
it is established weighting function of variables w, where
wi = 1; i = 0, 1, ..., n, because we do not have further information
on accuracy. Authors, Stastny and Skorpil proposed
in article [8] to solve the scale vector by the Least Mean
Square method. In our case, the matrix could have linear
dependence, but for the MOO purpose it is listed as the first
expression in Equation 5. Assume 𝔽 ≈ N ⋅ ε
and the residues r = 𝔽 − N ⋅ ε, and for the first use we expect that we know
all values observed on 𝔽 and also regard to the subject, partial
𝔽p and Np then we can take over basic equation of residua:
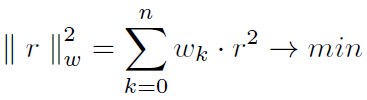 |
(5) |
4) Probability: as a weight let the probability ℘ of a occurrence 𝒟. For this calculation, we selected the Bayesian network approach and Markov’s analysis. Assume only two states:
- state = 1 ; a node is contested by 𝒟1
- state = 0 ; a node is not contested by 𝒟0
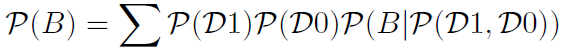 |
(6) |
Parallel is defined as only:
|
|
(7) |
Let us consider at the same time t as a constraint and that each node in N represents sub-input flow from G and is assigned in list Y, may be considered an idea, that the connection between each individual node νij is a two-subsystem and they have in start time t transition function h(t) = λto be contested. For example, take from the figure 3 node 2, which will be detected as contested by D in start time occurrence t, then is λ2,5< λ2,6. If the intensity of “contagion” is constant in time (t1; t2) between any two points, is solved differential equation in condition and the distribution is exponential F(t) = 1−e−λt and let set for the graph N global virtual time T, it can represent proper amount of cycles, then for selected node ν(i,j) with h(𝒟) ↣ ν(i,j): λ(t)h(𝒟) = t∈ T|T−1.
Summary, BN network is created, as is shown in Fig. 4, by lists of node ν, observability O = h(𝒟) of edge " and residual r(Contested; NotContested). If the node is not connected to edge ε, is not connected εi to the residual rj. The probability is set by p(εi | r1, ..., rn).
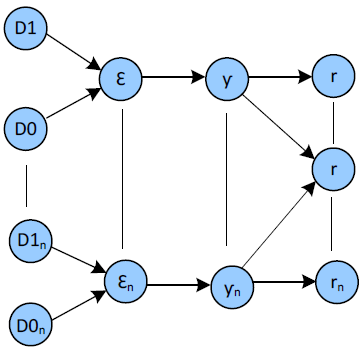
Fig. 4: Bayesian Network Model.
Is computed and then created matrix of probabilities p(t) on a space and for the MOO is selected:
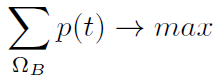 |
(8) |
5) Constraints and Objectives: The right computing of constraints is assumed to clear up after correction of mathematical formulas in the sections above. The first constraints to be defined are:
- constraint Y
- constraint in probability ℘
- constraint in 𝔽
- constraint in N;𝒟
CONCLUSION
The focus of this paper is on “Botnet Network”. The main objective is to propose steps to find appearances of a botnet network and illustrate how the NT can be potentially useful, nay, to measure the behavior of a network, but also for other activities such as botnet research and implement multi-objective algorithm to generate an efficient solution. These steps were defined in section A and are part of the mathematical formulas in section C. In a nutshell, two main weights for the calculation are defined. The first weight is the amount of excess flows with the NT combination and a second weight is selected the probability of “spreading” with exponential distribution. Than their costs (minimum) is proposed to search by MOO regards to two main objectives from equation of steps 3 and 4 and the solution is then intentioned to explicitly putt it in the NT. We still have to properly define the limits for multi-objective algorithm. Practical testing will follow. Finally, it would be interesting for further research to test a series of different systems and network form in order to see the efficiency and results between them and improve methods to predict the scope of contested nodes in a network. After this paper’s publishing, we hope to receive more ideas, and corrections from others to improve our conclusion on this subject.
Research described in this paper was financed by the National Sustainability Program under grant LO1401. For the research, infrastructure of the SIX Center was used.
REFERENCES
[1] VARDI, Y. Network Tomography: Estimating Source-Destination Traffic
Intensities from Link Data. Journal of the American Statistical Association.
1996, vol. 91, issue 433. DOI: 10.2307/2291416.
[2] UNIVERSITY OF CALIFORNIA’S SAN DIEGO SUPERCOMPUTER
CENTER. CAIDA: Center for Applied Internet Data Analysis [online].
2015 [cit. 2015-01-18]. Available: http://www.caida.org/home/
[3] RIPE NCC. RIPE Network Coordination Centre: RIPE Labs [online].
2015 [cit. 2015-01-26]. Available: https://labs.ripe.net/
[4] POLI, Riccardo, W LANGDON a Nicholas F MCPHEE. A field
guide to genetic programming [online]. [S.l.: Lulu Press], 2008, xiv,
233 s. [cit. 2015-01-25]. ISBN 978-1-4092-0073-4. Available: http://
www.gp-field-guide.org.uk/
[5] GEN, Mitsuo, Runwei CHENG a Lin LIN. Network models and optimization:
multiobjective genetic algorithm approach. London: Springer,
c2008, xiv, 692 p. ISBN 18-480-0180-0.
[6] MINARIK, M., STASTNY, J. Recognition of Randomly Deformed Objects.
In MENDEL 2008, 14th International Conference on Soft Computing.
Brno University of Technology, 2008, pp. 275-280, ISBN 978-80-
214-3675-6
[7] MEMON, Rashida A., Sameer QAZI a Adnan A. FAROOQUI. Network
tomography using genetic algorithms. TENCON 2012 IEEE Region
10 Conference [online]. IEEE, 2012, s. 1-6 [cit. 2015-01-14].
DOI: 10.1109/TENCON.2012.6412313. Available: http://ieeexplore.ieee.
org/lpdocs/epic03/wrapper.htm?arnumber=6412313
[8] STASTNY, J., SKORPIL, V. Analysis of Algorithms for Radial Basis
Function Neural Network. Personal Wireless Communications, Springer,
2007, volume 245, pp. 54-62, ISSN 1571- 5736, ISBN 978-0-387-74158-
1